Операторы координат, импульсов и их функций
& Литература: [8], [3], [1], [7].
Чтобы с помощью операторов получать наблюдаемые на опыте результаты, нужно установить, какие именно операторы следует сопоставлять тем или иным величинам. Установим вначале, какой оператор следует сопоставлять радиус-вектору частицы  . Для этого воспользуемся формулами (9.1), по которым вычисляются средние значения. В координатном представлении эти формулы дают:
. Для этого воспользуемся формулами (9.1), по которым вычисляются средние значения. В координатном представлении эти формулы дают:
á  ñ =
ñ = 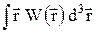 =
= 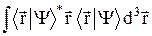 =
= 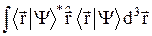 .
.
Из последнего равенства следует, что в качестве оператора 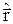 следует взять оператор умножения на
следует взять оператор умножения на  . Фактически установлен вид операторов координат:
. Фактически установлен вид операторов координат: 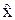 = x,
= x, 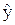 = y,
= y, 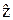 = z.
= z.
Оператор импульса 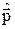 подбирается, исходя из того, что волна де Бройля, описывающая состояние с определенным импульсом
подбирается, исходя из того, что волна де Бройля, описывающая состояние с определенным импульсом 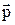 , должна быть собственной функцией оператора
, должна быть собственной функцией оператора 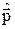 , соответствующей собственному значению
, соответствующей собственному значению 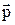 :
:
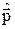
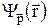 =
= 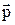
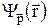 ,
, 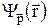 = A exp
= A exp 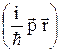 ,
, 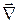
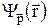 =
= 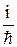
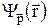 →
→
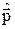 =–i ħ
=–i ħ 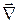 =–i ħ
=–i ħ  .
. 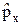 =–i ħ
=–i ħ 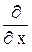 ,
, 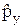 = –i ħ
= –i ħ 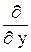 ,
, 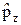 = –i ħ
= –i ħ 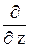 . (11.1)
. (11.1)
Итак, установлены операторы координат и импульсов. Они удовлетворяют следующим перестановочным соотношениям:
[x 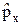 ] = i ħ, [x
] = i ħ, [x 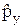 ] = [
] = [ 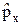
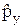 ] = [x y]=0, (11.2)
] = [x y]=0, (11.2)
а также аналогичным выражениям с заменой x→y→z→x.
Перестановочные соотношения имеют большое значение в квантовой механике. В соответствии с теоремой о коммутирующих операторах из (11.2) следует, что несовместными величинами являются координата и соответствующая ей проекция импульса. Для несовместных величин имеет место соотношение неопределенностей. Оно устанавливается следующей теоремой.
Если операторы величин F и G связаны с некоторым самосопряженным оператором  равенством [
равенством [ 
 ] = i
] = i  , то для неопределенностей этих величин DF и DG имеет место соотношение DF DG ≥ áKñ. (11.3)
, то для неопределенностей этих величин DF и DG имеет место соотношение DF DG ≥ áKñ. (11.3)
Смысл обозначений в (11.3) следующий: áKñ= 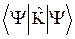 , DF =
, DF = 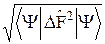 , где
, где 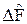 =
=  – áFñ, áFñ=
– áFñ, áFñ= 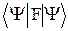 , величина DG аналогична DF.
, величина DG аналогична DF.
Для доказательства теоремы следует воспользоваться вспомогательным вектором ÷jñ = (a 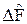 – i
– i 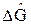 )÷Yñ, где a – действительное число, а i – мнимая единица. Скалярный квадрат этого вектора положителен. Он является функцией параметра a:
)÷Yñ, где a – действительное число, а i – мнимая единица. Скалярный квадрат этого вектора положителен. Он является функцией параметра a: 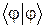 = f(a) = a2DF2 + a áKñ + DG2. При получении этого выражения следует учесть, что операторы
= f(a) = a2DF2 + a áKñ + DG2. При получении этого выражения следует учесть, что операторы 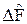 и
и 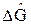 связаны такими же соотношениями, как и операторы
связаны такими же соотношениями, как и операторы  и
и  . Квадратный трехчлен f(a) положителен, если его дискриминант меньше нуля. Отсюда и получается соотношение (11.3).
. Квадратный трехчлен f(a) положителен, если его дискриминант меньше нуля. Отсюда и получается соотношение (11.3).
Применение данной теоремы к операторам координат и импульсов, для которых справедливы перестановочные соотношения (11.2), дает соотношение неопределенностей Гейзенберга Dx Dpx ≥ ħ / 2.
Построение операторов величин, которые в классической физике выражаются через координаты и импульсы, осуществляется по следующему правилу: соотношения между операторами физических величин такие же, как и между соответствующими величинами в классической физике. Это правило вместе с другими постулатами подтверждается согласием теории с практикой. Руководствуясь данным правилом, получим выражения для операторов потенциальной функции 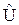 , кинетической энергии
, кинетической энергии 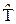 и оператора Гамильтона
и оператора Гамильтона  (гамильтониана):
(гамильтониана):
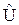 = U(
= U( 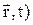 ,
, 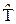 =
= 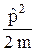 =
= 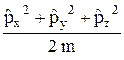 ,
,  =–
=– 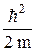
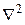 +
+ 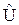 (
( 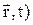 . (11.4)
. (11.4)
? Контрольные вопросы
1. Расскажите о подборе операторов координат.
2. Получите выражение для оператора импульса.
3. Какие из операторов координат и импульсов коммутируют, а какие нет?
4. Расскажите о физических следствиях перестановочных соотношений (11.2).
5. Что является обобщением соотношения неопределенностей Гейзенберга?
6. Какой точный смысл имеют величины, входящие в соотношение неопределенностей Гейзенберга?
7. Запишите оператор Гамильтона.
8. Совместны ли кинетическая и потенциальная энергии?
|
Д. 11.1.Коммутационные соотношения для операторов координат и импульсов.
Д. 11.2.Соотношение неопределенностей произвольных несовместных величин.
11.2. Состояние электрона описывается функцией
|

|
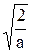 sin
sin 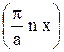 , если 0 £ x £ a
, если 0 £ x £ a
0, если x< 0, x > a.
Найти среднюю кинетическую энергию электрона в этом состоянии.
Дата добавления: 2021-11-16; просмотров: 495;











