Уравнение Шредингера. Стационарные состояния
& Литература: [1], [3], [7], [6].
Изменение состояния с течением времени описывается посредством законов эволюции. Таковыми в классической механике выступают, в частности, законы Ньютона. Аналогичную роль в квантовой механике играет уравнение Шредингера.
Фундаментальные уравнения теории постулируются. Однако появляются они в результате анализа известных ранее в науке положений.
К уравнению Шредингера можно придти, опираясь на выражение волны де Бройля: Y = A exp (– 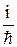 (E t –
(E t – 
 )). (14.1)
)). (14.1)
Функция (14.1) является собственной функцией оператора импульса 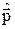 . Гамильтониан свободной частицы
. Гамильтониан свободной частицы  =
= 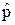 2 / (2 m) коммутирует с
2 / (2 m) коммутирует с 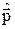 . Поэтому функция (14.1) является собственной также и для
. Поэтому функция (14.1) является собственной также и для  , то есть выполняется соотношение:
, то есть выполняется соотношение:  Y = E Y. (14.2)
Y = E Y. (14.2)
Разыскиваемые законы должны давать изменение вида Y-функции с течением времени. Поэтому целесообразно продифференцировать (14.1):
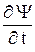 = –
= – 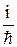 E Y. (14.3)
E Y. (14.3)
Подставляя сюда (14.2), получим: i ћ 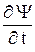 =
=  Y. (14.4)
Y. (14.4)
Предполагается, что это уравнение справедливо не только для волн де Бройля. Такая гипотеза успешно проходит испытание принципом соответствия: в тех случаях, когда величиной ħ можно пренебречь, из уравнения (14.4) получается уравнение Гамильтона–Якоби, описывающее движение классической частицы.
Постулируется, что уравнение (14.4) справедливо для любых Y-функций и любых  . Более того, это уравнение обобщается для произвольных квантовомеханических векторов состояния |Y>:
. Более того, это уравнение обобщается для произвольных квантовомеханических векторов состояния |Y>:
i ћ 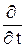 |Y> =
|Y> =  |Y>. (14.5)
|Y>. (14.5)
Истинность уравнения Шредингера (14.5) подтверждается согласием получаемых из него следствий с опытом.
Уравнение Шредингера описывает эволюцию системы и тем самым реализует принцип причинности.
Из уравнения Шредингера можно получить уравнение непрерывности: 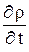 +
+ 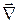
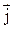 = 0, (14.6)
= 0, (14.6)
где r = Y* Y – плотность вероятности, а
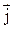 = –
= –  (Y*
(Y* 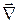 Y – Y
Y – Y 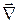 Y*) – (14.7)
Y*) – (14.7)
плотность потока вероятности.
Стационарным называют состояние, описываемое решением уравнения Шредингера с независимым от времени гамильтонианом. Для амплитуды (волновой функции) Y(B, t) стационарного состояния в представлении набора переменных B можно записать:
i ћ 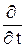 Y(B, t) =
Y(B, t) =  Y(B, t), (14.8)
Y(B, t), (14.8)
где 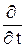
 (B, t) = 0. В координатном представлении B →
(B, t) = 0. В координатном представлении B → 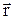 .
.
Амплитуда стационарного состояния может быть представлена в виде произведения временной и не временной частей:
Y(B, t) = Y(B) exp (– 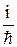 (E t)), (14.9)
(E t)), (14.9)
где Y(B) – решение стационарного уравнения Шредингера:
 Y(B) = E Y(B), (14.10)
Y(B) = E Y(B), (14.10)
а E – энергия системы.
Из (14.9) следует независимость от времени величины |Y(B, t)|2 = |Y(B)|2. Это означает, что в стационарном состоянии с течением времени не меняются распределение вероятностей тех или иных значений любых переменных B, а также их средние значения <B>.
В стационарных состояниях энергия E имеет определенные значения. Чтобы их найти, нужно решить стационарное уравнение Шредингера (14.10) и обеспечить выполнение условий, которым должна удовлетворять амплитуда состояния (волновая функция) Y(B, t).
? Контрольные вопросы
1. Запишите квантово-механическое уравнение движения. Расскажите о его смысле и значении.
2. Как получается уравнение Шредингера?
3. Запишите уравнение Шредингера для нерелятивистской частицы.
4. Расскажите об области применимости уравнения Шредингера.
5. Расскажите об уравнении непрерывности.
6. Расскажите о связи величин r и 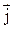 с плотностью электрического заряда и плотностью электрического тока.
с плотностью электрического заряда и плотностью электрического тока.
7. Какое состояние называют стационарным?
8. Как находится Y-функция стационарного состояния?
9. Перечислите свойства стационарных состояний.
|
14.1.Получите из уравнения Шредингера уравнение Гамильтона–Якоби.
14.2.Получите из уравнения Шредингера уравнение непрерывности.
14.3.Вычислите плотность потока вероятности для свободно движущегося со скоростью  электрона.
электрона.
14.4.Напишите уравнение Шредингера для частицы, движущейся вдоль оси x под действием квазиупругой силы с коэффициентом жесткости k.
14.5.Докажите, что амплитуда (14.9) удовлетворяет уравнению (14.8).
14.6.Выясните, является ли волновая функция
Y =  k(x) exp(–i wk t), представляющая собой суперпозицию стационарных состояний, решением полного и стационарного уравнений Шредингера.
k(x) exp(–i wk t), представляющая собой суперпозицию стационарных состояний, решением полного и стационарного уравнений Шредингера.
§15. Уравнение движения в форме Гейзенберга.
Интегралы движения
& Литература: [1], [3].
Уравнения движения в форме Гейзенберга позволяют судить об изменении той или иной величины непосредственно, без предварительного нахождения амплитуды состояния. Они учитывают то обстоятельство, что представляющая интерес величина может вообще не иметь определенного значения. Поэтому с их помощью находится изменение со временем среднего значения величины.
Вводится оператор  Û
Û  производной величины F по времени такой, что для любого состояния |Y>
производной величины F по времени такой, что для любого состояния |Y>
< 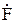 > Û <Y|
> Û <Y|  |Y> =
|Y> =  <F> Û
<F> Û  <Y|
<Y| 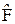 |Y>. (15.1)
|Y>. (15.1)
Именно этот оператор и удовлетворяет уравнению движения в форме Гейзенберга:  =
=  =
=  + {
+ {  ,
, 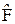 }, (15.2)
}, (15.2)
где {  ,
, 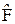 } =
} = 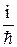 [
[  ,
, 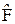 ] =
] = 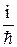 [
[ 
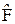 –
– 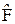
 ] – (15.3)
] – (15.3)
квантовые скобки Пуассона.
Уравнение (15.2) отражает то обстоятельство, что изменение среднего значения <F> величины F может происходить вследствие изменения со временем вида самого оператора, а также вследствие перераспределения величины F по ее возможным значениям.
Величина F, для которой  = 0, называется интегралом движения.
= 0, называется интегралом движения.
Для того чтобы величина F была интегралом движения, достаточно, чтобы ее оператор явно не зависел от времени и чтобы он коммутировал с оператором Гамильтона.
? Контрольные вопросы
1. Что имеют общего и чем отличаются друг от друга уравнения движения в форме Шредингера и в форме Гейзенберга?
2. Какой смысл имеет оператор производной физической величины по времени?
3. Какой смысл имеет каждое слагаемое в правой части уравнения (15.2)?
4. Что имеют общего и чем отличаются друг от друга интегралы движения в квантовой механике и в классической физике?
5. Как узнать, является ли та или иная величина в определенных условиях интегралом движения или нет? Приведите примеры.
|
17.1.Докажите следующие операторные равенства:
 (
( 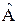 +
+ 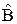 ) =
) =  +
+ 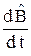 ;
;  (
( 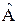
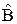 ) =
) = 
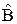 +
+ 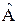
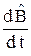 .
.
17.2.Какие из механических величин (E, Px, Py Pz) сохраняются при движении частицы: а) в отсутствии поля; б) в поле с потенциальной функцией U = a z?
17.3.Покажите, что в центральном поле квадрат момента импульса L2 и его проекция Lz являются интегралами движения. Оператор 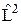 в сферических координатах имеет вид (22.3), а
в сферических координатах имеет вид (22.3), а 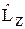 = – i ħ
= – i ħ 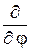 .
.
Дата добавления: 2021-11-16; просмотров: 501;











