Свойства амплитуд состояний
& Литература: [8], [3], [7].
Какими свойствами должны обладать введенные для описания состояния s амплитуды áBïsñ? Поскольку они пропорциональны вероятностям Ws(B) тех или иных значений величин B в данном состоянии, то можно записать: ÷áBïsñç2 = N Ws(B), (6.1)
где N – произвольное положительное число. Сложив все равенства (6.1), получим: 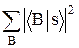 = N
= N 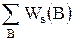 = N, (6.2)
= N, (6.2)
так как обнаружение хоть какого-то значения переменных B – событие достоверное. Коэффициент 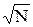 называется нормой амплитуды состояния. Из-за произвола числа N амплитуды состояния определяются с точностью до произвольного комплексного множителя k, то есть амплитуды k áBïsñ и áBïsñ описывают одно и то же состояние, так как дают те же самые значения Ws(B).
называется нормой амплитуды состояния. Из-за произвола числа N амплитуды состояния определяются с точностью до произвольного комплексного множителя k, то есть амплитуды k áBïsñ и áBïsñ описывают одно и то же состояние, так как дают те же самые значения Ws(B).
Если переменные B имеют непрерывный спектр значений, то амплитуда состояния представляет собой волновую функцию áBïsñ = Ys(B). В этом случае квадрат модуля амплитуды характеризует плотность вероятности rs(B) определенного значения B:
÷áBïsñç2 = ÷Ys(B)ñç2 = N 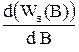 = N rs(B). (6.3)
= N rs(B). (6.3)
Здесь квадрат нормы волновой функции N = 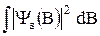 . (6.4)
. (6.4)
Интегрирование производится по всей области значений переменных B.
Так как амплитуды состояния определяются с точностью до произвольного множителя, то норму 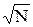 можно чаще всего сделать равной единице, что упрощает формулы (6.1) и (6.3). Такая процедура называется нормировкой амплитуды состояния на единицу. В случае непрерывного спектра нормировка на единицу не возможна, если интеграл (6.4) равен бесконечности.
можно чаще всего сделать равной единице, что упрощает формулы (6.1) и (6.3). Такая процедура называется нормировкой амплитуды состояния на единицу. В случае непрерывного спектра нормировка на единицу не возможна, если интеграл (6.4) равен бесконечности.
В соответствии с физическим смыслом амплитуды состояния волновая функция должна удовлетворять стандартным условиям: быть непрерывной, однозначной и конечной.
Чтобы амплитуды состояния обеспечивали вероятностное поведение микрочастиц, они должны удовлетворять следующему принципу суперпозиции. Если микрообъект может находиться в состояниях, описываемых амплитудами áBïA1ñ, áBïA2ñ, …áBïAiñ, то он может находиться и в состоянии, описываемым линейной комбинацией этих амплитуд:
áBïsñ = 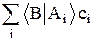 , (6.5)
, (6.5)
где ci – произвольные комплексные числа.
Соотношение (5.1) представляет собой частный случай формулы (6.5) применительно к интерференции электронов на двух щелях. Так что принцип суперпозиции отражает корпускулярно-волновой дуализм микрочастиц. В отличие от суперпозиции интерферирующих волн, в которых колеблющиеся величины могут принимать любые значения, суперпозиция амплитуд относится и к таким состояниям, в которых величины принимают дискретный ряд значений.
Принцип суперпозиции дополняется принципом умножения амплитуд, отражающим теорему об умножении вероятностей:
áBïsñi = áBïAiñ áAiïsñ. (6.6)
Это равенство означает, что амплитуда перехода из состояния s в состояние B через промежуточное состояние Ai равна произведению амплитуды перехода из s в Ai и амплитуды перехода из Ai в B. Слагаемые в (6.5) и представляют собой амплитуды перехода из s в B через промежуточные состояния Ai. Так что ci = áAiïsñ и получается правило композиции амплитуд:
áBïsñ = 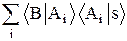 . (6.7)
. (6.7)
Амплитуда áBïsñ составляется из амплитуд некоторых базисных состояний áBïAiñ.
Можно ли применить формулу (6.7) для произвольного состояния áBïsñ? Для некоторых базисов áBïAiñ это можно сделать. Такие базисы называют полными. Для того, чтобы базис был полным, необходимо выполнение условий:
áAjïAiñ = dij, где dij = 1, если i = j и dij = 0, если i 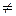 j. (6.8)
j. (6.8)
Базис, удовлетворяющий условиям (6.8) называют ортонормированным.
Чтобы убедиться в справедливости соотношений (6.8) для полного базиса, применим формулу (6.7), справедливую для произвольного состояния, к амплитуде перехода в базисное состояние Aj:
áAjïsñ = 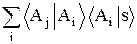 . (6.9)
. (6.9)
Из этого равенства и следует (6.8).
В дальнейшем мы будем иметь дело с состояниями, образующими ортонормированные и полные базисы. По таким базисам можно разложить произвольное состояние, применив правило композиции амплитуд (6.7). Это правило позволяет также перейти от одного представления состояния s к другому: Зная все амплитуды вероятности áAiïsñ, можно получить амплитуду состояния áBïsñ.
На амплитуды вероятности накладывается еще одно требование – условие эрмитовой симметрии: áBïAñ* = áAïBñ. (6.10)
Это условие отражает обратимость процессов в микромире: вероятность перехода в состояние B из состояния A равна вероятности обратного перехода. С помощью (6.10) и правила композиции более компактно и естественно можно записать условие нормировки состояния на единицу:
N = 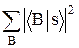 =
= 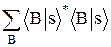 =
= 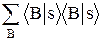 = ásïsñ = 1.
= ásïsñ = 1.
Это условие вполне естественно, поскольку амплитуда ásïsñ описывает достоверное событие.
Правило композиции применяется с некоторыми коррективами и в случае, когда базисные состояния образуют несчетное множество. В качестве таких состояний часто используют волны де Бройля:
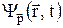 =
= 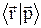 = A exp
= A exp 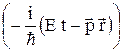 . (6.11)
. (6.11)
Поскольку импульс 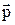 может быть любым, то число волн де Бройля не ограничено. Корректировка применения правила композиции для несчетного множества базисных состояний сводится к замене суммирования в формуле (6.7) к интегрированию. Кроме того, в условии полноты базиса (6.8) вместо символа Кронекера используется функция Дирака:
может быть любым, то число волн де Бройля не ограничено. Корректировка применения правила композиции для несчетного множества базисных состояний сводится к замене суммирования в формуле (6.7) к интегрированию. Кроме того, в условии полноты базиса (6.8) вместо символа Кронекера используется функция Дирака:
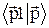 = d
= d 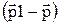 . (6.12)
. (6.12)
Функция Дирака векторного аргумента равна произведению функций Дирака от проекций этого аргумента:
d 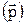 = d(px) d(py) d(pz). (6.13)
= d(px) d(py) d(pz). (6.13)
Для одномерной функции Дирака справедливы соотношения:
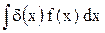 = f (0), (6.14)
= f (0), (6.14)
d(x) = 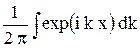 . (6.15)
. (6.15)
Чтобы обеспечить для волн де Бройля (6.11) необходимое условие (6.12) полноты базиса, на множитель A в (6.11) должно быть наложено условие
úAç= 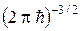 . (6.16)
. (6.16)
Чтобы убедиться в этом, следует применить к левой части (6.12) правило композиции и использовать соотношения (6.15):
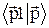 =
= 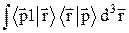 =
= 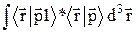 =
=
= úAç2 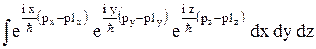 =
=
=úAç2 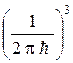 d(px–p1x) d( py–p1y) d( pz–p1z) = úAç2
d(px–p1x) d( py–p1y) d( pz–p1z) = úAç2 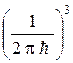 d
d 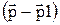 .
.
Используя волны де Бройля с найденным значением множителя A, можно переходить от координатного представления амплитуды состояния к импульсному и наоборот.
? Контрольные вопросы
1. Назовите свойства амплитуд состояния.
2. Что такое норма состояния?
3. Как вычисляется норма волновой функции?
4. На чем основана и как осуществляется нормировка амплитуды состояния на единицу?
5. Сформулируйте квантовомеханический принцип суперпозиции. Сравните его с классическим принципом суперпозиции.
6. В чем заключается правило умножения амплитуд?
7. При каких условиях правило композиции можно применять к произвольному состоянию?
8. Каков физический смысл условий ортонормированности базисных состояний?
9. Как изменится амплитуда вероятности, если поменять местами индексы состояния и представления?
10. Как осуществляется нормировка волн де Бройля?
11. Расскажите о d-функции и ее свойствах.
12. Запишите разложение произвольной волновой функции Y( 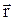 , t) по волнам де Бройля.
, t) по волнам де Бройля.
|
6.1. Докажите, что амплитуды состояния определяются с точностью до произвольного комплексного множителя.
6.2. Выведите формулу (6.16).
6.4. Нужно ли накладывать какие-либо ограничения на функцию
A 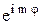 (j – сферическая координата) для того, чтобы эта функция могла быть волновой функцией? m = 0, ±1, ±2, ±3, ….
(j – сферическая координата) для того, чтобы эта функция могла быть волновой функцией? m = 0, ±1, ±2, ±3, ….
6.5. Состояние электрона описывается функцией
|
|
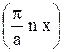 , если 0 £ x £ a
, если 0 £ x £ a
0, если x< 0, x > a.
Пронормировать эту функцию. Построить и проанализировать график плотности вероятности нахождения электрона в различных точках пространства.
6.6. Найти нормировочный коэффициент N для волновой функции основного состояния атома водорода Y( 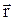 ) = N exp(–r / r0). N = (p r03)–1/2.
) = N exp(–r / r0). N = (p r03)–1/2.
6.7. Нарисовать график функции d (K, x) = 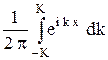 и исследовать поведение его при увеличении параметра K.
и исследовать поведение его при увеличении параметра K.
6.8. Амплитуда нормированного на единицу состояния s представлена в виде áBïsñ = 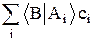 . Найти
. Найти 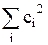 .
.
6.9. Найти волновую функцию в 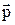 и в
и в  -представлениях для частицы, локализованной в точке
-представлениях для частицы, локализованной в точке 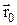 . (2 p ħ)–3/2 exp
. (2 p ħ)–3/2 exp 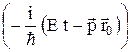 ; d(
; d(  –
– 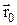 ).
).
6.10. Найти волновую функцию в импульсном представлении, которая соответствует волновому пакету прямоугольной формы:

|
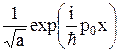 , если –a/2 £ x £ a/2
, если –a/2 £ x £ a/2
0, если úxç > a/2.
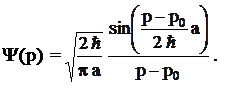 6.11. Электрон находится в состоянии, описываемом волновой функцией
6.11. Электрон находится в состоянии, описываемом волновой функцией
Y(x, t) = A cos 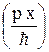 exp
exp 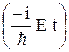 .
.
Какие значения импульса будут зарегистрированы в этом состоянии?
Векторы состояний
& Литература: [8], [3], [7].
Векторный формализм оказался очень удобным во всех разделах физики. Он позволил компактно записывать законы, использовать наглядные геометрические образы и соотношения. П. Дирак нашел способ распространить векторный формализм и на квантовую механику. Такую возможность он нашел, анализируя правило композиции амплитуд. Использованные выше скобочные обозначения Дирака введены им именно при разработке векторного формализма квантовой механики.
Благодаря правилу композиции амплитуда перехода в состояние B из состояния A оказывается аналогичной скалярному произведению векторов B и A. Чтобы увидеть эту аналогию, амплитуду перехода представим в следующем виде:
áBïAñ = 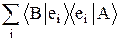 =
= 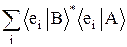 =
= 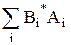 , где (7.1)
, где (7.1)
Bi* =áeiïBñ* = áBïeiñ, а Ai = áeiïAñ, причем áeiïejñ = dij. (7.2)
Скалярному произведению векторных величин 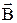 и
и 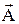 тоже можно придать вид, аналогичный (7.1): (
тоже можно придать вид, аналогичный (7.1): ( 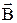 ,
, 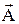 ) =
) = 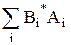 , (7.3)
, (7.3)
если обозначить Bi*= ( 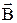 ,
, 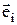 ) и Ai = (
) и Ai = ( 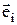 ,
, 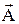 ), где
), где 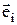 – ортонормированные базисные векторы, для которых справедливо условие (
– ортонормированные базисные векторы, для которых справедливо условие ( 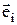 ,
, 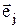 ) = dij. Так что символы B и A в (7.1) и (7.2) аналогичны векторным величинам
) = dij. Так что символы B и A в (7.1) и (7.2) аналогичны векторным величинам 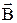 и
и 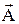 , а ei – базисным векторам
, а ei – базисным векторам 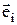 . Полной аналогии амплитуд áBïAñ и скалярных произведений (
. Полной аналогии амплитуд áBïAñ и скалярных произведений ( 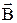 ,
, 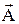 ) препятствует то обстоятельство, что перестановка сомножителей в скалярном произведении не влияет на результат, а перестановка индексов амплитуды вероятности дает комплексно сопряженное значение.
) препятствует то обстоятельство, что перестановка сомножителей в скалярном произведении не влияет на результат, а перестановка индексов амплитуды вероятности дает комплексно сопряженное значение.
В математике понятие вектор шире понятия векторной физической величины. Рассматриваются векторы и в комплексном пространстве. Для таких векторов скалярное произведение при перестановке сомножителей заменяется комплексно сопряженным числом. Так что имеется полная аналогия амплитуд вероятности и скалярных произведений векторов комплексного пространства. Число базисных состояний ei в разложении (7.1) может быть неограниченным. Комплексное векторное пространство с неограниченным числом базисных состояний, называемое гильбертовым пространством, Дирак предложил использовать для описания состояний микрообъектов.
Каждому состоянию микрообъекта A ставится в соответствие вектор гильбертова пространства так, что скалярное произведение векторов является амплитудой перехода между соответствующими состояниями. Вектор состояния обозначается ÷Añ и называется cket-вектором. Скалярное произведение векторов ÷Bñ и ÷Añ имеет смысл амплитуды áBïAñ:
(÷Bñ,÷Añ) = áBïAñ. (7.4)
Перестановка сомножителей согласуется со свойством эрмитовой симметрии амплитуд (6.10): (÷Añ,÷Bñ) = áAïBñ = (÷Bñ,÷Añ)* = áBïAñ*.
В пространстве cket-векторов может быть выбран базис ÷eiñ, для которого выполняется условие (÷eiñ,÷ejñ) = áeiïejñ = dij. Любой вектор ÷Añ можно разложить по базису, то есть представить в виде ÷Añ = 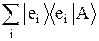 , аналогично тому, как геометрический вектор
, аналогично тому, как геометрический вектор 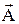 выражается через его проекции:
выражается через его проекции: 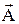 = Ax
= Ax 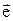 x+Ay
x+Ay 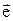 y+Az
y+Az 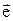 z. Амплитуды áeiïAñ аналогичны проекциям геометрического вектора на координатные оси. Совокупность координат (Ax, Ay, Az) задает геометрический вектор
z. Амплитуды áeiïAñ аналогичны проекциям геометрического вектора на координатные оси. Совокупность координат (Ax, Ay, Az) задает геометрический вектор 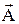 . Аналогично совокупность всех амплитуд áeiïAñ задает состояние A в e- представлении.
. Аналогично совокупность всех амплитуд áeiïAñ задает состояние A в e- представлении.
Комплексному пространству ставится в соответствие сопряженное с ним пространство (по терминологии Дирака – пространство bra-векторов, или bra- пространство). Bra-векторы обозначаются символом áAï. Скалярное произведение векторов áBï и áAï является величиной комплексно сопряженной скалярному произведению соответствующих cket-векторов:
(áBï,áAï) = (÷Bñ,÷Añ)* = áBïAñ* = áAïBñ. (7.5)
Скалярное произведение квантово-механических векторов выражается амплитудой, которая изображается в виде записанных рядом bra- и cket- векторов так, чтобы в результате получилась bracket (скобка).
Таким образом, состояние микрообъекта Y описывается или bra-вектором áYï, или сопряженным ему cket-вектором ïYñ. Переход от одного из сопряженных пространств к другому называют операцией эрмитова сопряжения и обозначают символом «+»:
ïYñ+ = áYï; áBïAñ+= áAïBñ = áBïAñ*.
Применительно к амплитудам (комплексным числам) операция эрмитова сопряжения совпадает с операцией комплексного сопряжения.
Состояние Y можно также описать множеством проекций вектора состояния на базисные векторы ÷Вjñ: áВiïYñ, или, опуская индекс i, áВïYñ. Это множество комплексных чисел есть амплитуда состояния Y в B-представлении. Амплитуды одного и того же состояния различны в различных представлениях подобно тому, как различны проекции одного и того же геометрического вектора в различных координатных системах.
Если переменные набора B имеют непрерывный спектр, то амплитуда состояния представляет собой функцию непрерывно меняющихся переменных B: áBïYñ = Y(B) – волновую функцию. В квантовой механике часто используется координатное представление, при котором переменные B смеют смысл декартовых координат радиус-вектора точки  : á
: á  ïYñ = Y(
ïYñ = Y(  ). Именно такой способ описания состояния микрочастицы был первоначально предложен M. Борном.
). Именно такой способ описания состояния микрочастицы был первоначально предложен M. Борном.
Дираковский формализм удобен для записи основных соотношений квантовой механики. Соотношения оказываются компактными, инвариантными, то есть не зависят от выбора представлений. Для получения же проверяемых экспериментально результатов нужно использовать конкретное представление, чаще всего используется координатное представление.
? Контрольные вопросы
1. На чем основан векторный формализм описания состояния микрообъектов?
2. Расскажите о cket-векторах.
3. Расскажите о bra-векторах.
4. Какой смысл имеют проекции векторов состояний на базисные векторы?
5. Перечислите способы описания состояний микрообъектов.
6. Когда целесообразно использовать те или иные способы описания состояния микрообъектов?
|
7.1. Запишите скалярное произведение векторов состояния úYñ и újñ в координатном представлении.
7.2. Запишите в координатном представлении условие нормировки вектора состояния úYñ на единицу.
7.3. Запишите волну де Бройля в координатном и в импульсном представлениях, используя формализм Дирака.
Дата добавления: 2021-11-16; просмотров: 567;











