Методы проверки статистических гипотез

Выводы из любого сельскохозяйственного или биологического эксперимента нужно оценить с учетом их значимости, или существенности. Такую оценку проводят путем сравнения вариантов опыта друг с другом, либо с контролем (стандартом), или с теоретически ожидаемым распределением.

Статистическая гипотеза – научное предположение о тех или иных статистических законах распределения рассматриваемых случайных величин, которое может быть проверено на основе выборки. Сравнивают совокупности путем проверки нулевой гипотезы – об отсутствии реального различия между фактическими и теоретическими наблюдениями, пользуясь наиболее подходящим статистическим критерием. Если в результате проверки различия между фактическими и теоретическими показателями близки к нулю или находятся в области допустимых значений, то нулевая гипотеза не опровергается. Если же различия оказываются в критической для данного статистического критерия области, невозможны при нашей гипотезе и поэтому несовместимы с ней, нулевая гипотеза опровергается.

Принятие нулевой гипотезы означает, что данные не противоречат предположению об отсутствии различий между фактическими и теоретическими показателями. Опровержение гипотезы означает, что эмпирические данные несовместимы с нулевой гипотезой и верна другая, альтернативная гипотеза. Справедливость нулевой гипотезы проверяется вычислением статистических критериев проверки для определенного уровня значимости.

Уровень значимости характеризует, в какой мере мы рискуем ошибиться, отвергая нулевую гипотезу, т.е. какова вероятность отклонения от установленных пределов варьирования случайной величины. Поэтому, чем больше уровень вероятности, тем меньше уровень значимости.

Понятие о вероятности неразрывно связано с понятием о случайном событии. В сельскохозяйственных и биологических исследованиях вследствие присущей живым организмам изменчивости под влиянием внешних условий появление события может быть случайным либо неслучайным. Неслучайными будут такие события, которые выходят за пределы возможных случайных колебаний выборочных наблюдений. Это обстоятельство позволяет определить вероятность появления как случайных, так и неслучайных событий.

Таким образом, вероятность – мера объективной возможности события, отношение числа благопрятных случаев к общему числу случаев. Уровень значимости показывает вероятность, с которой проверяемая гипотеза может дать ошибочный результат. В практике сельскохозяйственных исследований считается возможным пользоваться вероятностями 0,95 (95 %) и 0.99 (99 %), которым соответствуют следующие уровни значимости 0,05 – 5 % и 0,01 – 1 %. Эти вероятности получили название доверительных вероятностей, т.е. таких, которым можно доверять.

Статистические критерии, используемые для оценки расхождения между статистическими совокупностями, бывают двух видов:

1) параметрические (для оценки совокупностей, имеющих нормальное распределение);

2) непараметрические (применяют к распределениям любой формы).

В практике сельскохозяйственных и биологических исследований встречаются два типа опытов.

В некоторых опытах варианты связаны друг с другом одним или несколькими условиями, контролируемыми исследователем. Вследствие этого опытные данные варьируют не независимо, а сопряженно, так как влияние условий, связывающих варианты, проявляется, как правило, однозначно. К такого типа опытам относятся, например, полевое испытание с повторностями, каждая из которых располагается на участке сравнительно одинакового плодородия. В таком опыте сопоставлять варианты друг с другом можно только в пределах повторения. Другой пример связанных наблюдений – изучение фотосинтеза; здесь объединяющим условием являются особенности каждого подопытного растения.

Наряду с этим часто сравнивают совокупности, варианты которых изменяются независимо друг от друга. Несопряженными, независимыми являются варьирование признаков растений, выращенных в разных условиях; в вегетационных опытах повторностями служат сосуды одноименных вариантов, и любой сосуд одного варианта можно сравнивать с любым сосудом другого.

Статистическая гипотеза– некоторое предположение о законе распределения случайной величины или о параметрах этого закона в рамках данной выборки.

Пример статистической гипотезы: "генеральная совокупность распределена по нормальному закону", "различие между дисперсиями двух выборок незначимо" и т.д.

При аналитических расчетах часто необходимо выдвигать и проверять гипотезы. Проверка статистической гипотезы осуществляется с помощью статистического критерия в соответствии со следующим алгоритмом:

Гипотеза формулируется в терминах различия величин. Например, есть случайная величина x и константа a.

Необходимо отметить, что знаки ≥, ≤, = здесь используются не в арифметическом, а в «статистическом» смысле. Их необходимо читать «значимо больше», «значимо меньше», «различие незначимо».

Метод по критерию t-Стъюдента.При сравнении средних двух независимых выборок применяют метод по t – критерию Стьюдента, предложенный английским ученым Ф. Госсетом. С помощью данного метода оценивается существенность разности средних (d = x₁ – x₂). Он основан на расчете фактических и табличных значений и их сравнении.

В теории статистики ошибка разности или суммы средних арифметических независимых выборок при одинаковом числе наблюдений (n₁ + n₂) определяется по формуле:

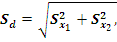
где S_d – ошибка разности или суммы;

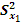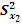и – ошибки сравниваемых средних арифметических.

Гарантией надежности вывода о существенности или несущественности различий между средними арифметическими служит отношение разницы к ее ошибке. Это отношение получило название критерия существенности разности:

t = x₁ – x₂ / 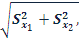= d / S_d.

Теоретическое значение критерия t находят по таблице, зная число степеней свободы Y = n₁ + n₂ – 2 и принятый уровень значимости.

Если t_факт ≥ t_теор , нулевая гипотеза об отсутствии существенности различий между средними опровергается, а если различия находятся в пределах случайных колебаний для принятого уровня значимости – не опровергается.

Метод интервальной оценки.Интервальная оценка характеризуется двумя числами – концами интервала, покрывающего оцениваемый параметр. Для этого следует определить доверительные интервалы для возможных значений средней генеральной совокупности. При этом, x является точечной оценкой генеральной средней, тогда точечную оценку генеральной средней можно записать так: x ± t_0,5×S_X, где t_0,5×S_X предельная ошибка выборочной средней при данном числе степеней свободы и принятом уровне значимости.

Доверительный интервал – это такой интервал, который с заданной вероятностью покрывает оцениваемый параметр. Центр интервала – выборочная оценка точки. Пределы, или доверительные границы, определяются средней ошибкой оценки и уровнем вероятности – x - t_0,5*S_X и x + t_0,5*S_X. Значение критерия Стьюдента для различных уровней значимости и числа степеней свободы приводятся в таблице.

Оценка разности средних сопряженных рядов.Оценку разности средних для сопряженных выборок вычисляют разностым методом. Сущность состоит в том, что оценивается существенность средней разности путем попарного сравнения вариантов опыта. Для нахождения S_d разностным методом вычисляют разность между сопряженными парами наблюдений d, определяют значение средней разности (d = Σ d / n) и ошибку средней разности по формуле:

S_d = √ Σ (d - d) ₂ / n (n – 1)

Критерий существенности вычисляют по формуле: t = d / S_d . Число степеней свободы находят по равенству Y= n-1, где n-1 – число сопряженных пар.