Статистические характеристики качественной изменчивости

Наряду с широко распространенным типом количественной изменчивости имеется немало случаев, когда различия между вариантами изучаемой статистической совокупности характеризуются качественными характеристиками.

Во всех случаях качественного варьирования распределение вариант по тому или иному признаку сводится, в конечном счете, к двум группам: окраска цветков у гибридных растений может быть выражена белая и розовая; красная и не красная; женские и мужские растения; здоровые и больные растения.

Поэтому такое качественное варьирование называется еще альтернативным (от французского – чередование, выбор, одно из двух), т.е. когда реализация одной из возможных альтернатив исключает тем самым возможность реализации другой.

Статистическая обработка полученных данных при альтернативной качественной изменчивости сводится к изучению количественного соотношения между обеими группами и установления процента наличия p и процента отсутствия q исследуемого явления.

Основные статистические показатели качественной изменчивости:

доля признака – p и q,

показатель изменчивости – S,

коэффициент вариации –V,

ошибка выборочной доли – S_p

Доля признака (относительная численность) отдельной варианты в данной совокупности и обозначается через p₁, p₂, p₃…. P_n. Выражается доля признака в частях единицы или в %. В первом случае сумма всех долей в пределах совокупности составляет 1, а во втором случае – 100%.

Доля признака – это отношение численности каждого из членов ряда n₁, n₂, n₃, ….n_n к численности N. Иными словами, доля признака – это вероятность появления данного признака в изучаемой совокупности:

p₁ = n₁ / N; p₂ = n₂ / N; и т.д.

Поскольку при альтернативной изменчивости доля одного признака равна - p, второго - q, вероятность двух противоположных явлений может быть выражена равенством p + q = 1 (100), а доля второго признака на основании равенства будет q = 1 – p.

Показатель изменчивости качественного признака (S), характеризующий варьирование величин ряда относительно друг друга, служит мерой степени варьирования и определяется по формуле:

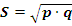
Так как сумма процентных выражений частот обеих альтернатив всегда равна 100 %, то значение среднего квадратического отклонения, выраженное в процентах, изменяется в пределах от 0-50 %. В зависимости от соотношения p и q значение S изменяется от 0-0,5. Если количество градаций признака больше двух, то S определяется по формуле:

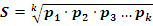
Коэффициент вариации качественных признаков 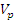– это показатель изменчивости, выраженный в % к максимальной изменчивости:

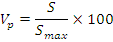
Коэффициент вариации характеризует относительную степень изменчивости исследуемых признаков и используется для сравнительной оценки выравненности различных совокупностей.

Ошибка выборочной доли (S_P)– это мера отклонения доли признака выборочной совокупности от доли его во всей генеральной совокупности вследствие неполной представительности выборки. Вычисляется по формуле:

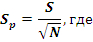
S – показатель изменчивости качественного признака;

N – объем выборки.

В современной теории статистики качественные (номинальные) признаки занимают особое положение и представляют собой единственный случай, когда объекту невозможно присвоить какое-либо цифровое значение. Градации номинального признака нельзя даже расположить в виде какого-то более или менее упорядоченного набора. Лишь две математические операции сравнения могут быть применены для признаков такого типа – «равно» и «не равно».

Такие признаки еще называют альтернативными, поскольку их вариации взаимно независимы и каждая – есть элемент ограниченного набора возможных альтернатив. При этом наличие только двух альтернативных вариант («да» или «нет», « 0» или « 1», «+» или «–») занимает особое положение и в этом случае признаки называют диморфными, т.е. имеющими только две вариации (морфы). В случае присутствия нескольких вариаций, признаки называются полиморфным (в узком понимании этого слова).

Особенности изменчивости объекта на основе анализа его номинальных признаков также может быть охарактеризовано функцией распределения. Для диморфных признаков эта функция определяется законом биномиального распределения, а для полиморфных – полиномиального распределения.