Типы статистического распределения

Частота проявления определенных значений признака в совокупности называется распределением. Различают эмпирические и теоретические распределения частот совокупности результатов наблюдений. Эмпирическое распределение – это распределение результатов измерений, полученных при изучении выборки. Теоретическое распределение предполагает распределение измерений на основании теории вероятностей. К их числу относятся: нормальное (Гауссово) (рис.23) распределение, распределение Стьюдента (рис.23) (t – распределение), F – распределение, распределение Пуассона, биноминальное.

Наибольшее значение в биологических исследованиях имеет нормальное или Гауссово (рис) распределение – это совокупность измерений, в котором варианты группируются вокруг центра распределения и их частоты равномерно убывают вправо и влево от центра распределения (x). Отдельные варианты отклоняются от средней арифметической симметрично, и размах вариации в обе стороны не превышает 3 σ . Нормальное распределение характерно для совокупностей, на членов которых суммарно влияет бесконечно большое количество разнообразных и разнонаправленных факторов. Каждый фактор вносит определенную часть в общую изменчивость признака. Бесконечные колебания факторов обусловливают изменчивость отдельных членов совокупностей.

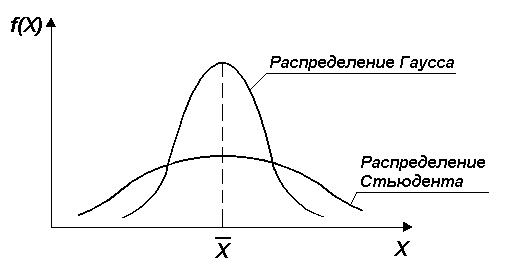
Рисунок 23 – Распределение Гаусса и Стьюдента

Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (а руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсетта вышла в журнале «Биометрика» под псевдонимом «Student» (Студент).

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Результатом игнорирования ограничений для t-критерия Стьюдента является заблуждение авторов статей и диссертаций, а далее и читателей этих публикаций, относительно истинного соотношения генеральных средних сравниваемых групп. Так в одном случае принимается вывод о значимом различии средних, когда они на самом деле не различаются, в другом – наоборот, принимается вывод об отсутствии значимого различия средних, когда такое различие имеется.

Нормальное распределение важно по многим причинам. Распределение многих статистик является нормальным или может быть получено из нормальных с помощью некоторых преобразований. Нормальное распределение представляет собой одну из эмпирически проверенных истин относительно общей природы действительности и его положение может рассматриваться как один из фундаментальных законов природы. Точная форма нормального распределения (характерная «колоколообразная кривая») определяется только двумя параметрами: средним и стандартным отклонением.

Характерное свойство нормального распределения состоит в том, что 68 % всех его наблюдений лежат в диапазоне ± 1 стандартное отклонение от среднего, а диапазон ; ± 2 стандартных отклонения содержит 95% значений. Другими словами, при нормальном распределении, стандартизованные наблюдения, меньшие -2 или большие +2, имеют относительную частоту менее 5% (Стандартизованное наблюдение означает, что из исходного значения вычтено среднее и результат поделен на стандартное отклонение (корень из дисперсии)). Если у вас имеется доступ к пакету STATISTICA, Вы можете вычислить точные значения вероятностей, связанных с различными значениями нормального распределения, используя Вероятностный калькулятор; например, если задать z-значение (т.е. значение случайной величины, имеющей стандартное нормальное распределение) равным 4, соответствующий вероятностный уровень, вычисленный STATISTICA будет меньше .0001, поскольку при нормальном распределении практически все наблюдения (т.е. более 99,99%) попадут в диапазон ± 4 стандартных отклонения.

Графическое выражение этого распределения называется Гауссовой кривой, или кривой нормального распределения. Опытным путем установлено, что такая кривая часто повторяет форму гистограмм, получающихся при большом числе наблюдений.

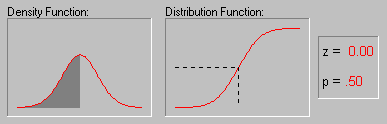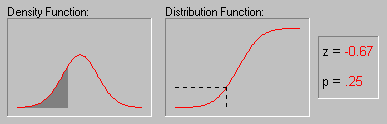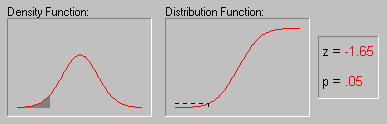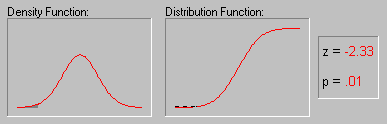
Форма кривой нормального распределения и ее положение определяются двумя величинами: генеральной средней и стандартным отклонением.

В практических исследованиях непосредственно формулой не пользуются, а прибегают к помощи таблиц.

Максимум, или центр, нормального распределения лежит в точке x = μ точка перегиба кривой находится при x1= μ - σ и x2= μ + σ , при n = ± ∞ кривая достигает нулевого значения. Размах колебаний от μ вправо и влево зависит от величины σ и укладывается в пределах трех стандартных отклонений:

1. В области пределов μ + σ находится 68,26% всех наблюдений;

2. Внутри пределов μ + 2 σ находится 95,46% всех значений случайной величины;

3. В интервале μ + 3σ находится 99,73%, практически все значения признака.

Однако по мере увеличения размера выборки, используемой для получения распределения выборочного среднего, это распределение приближается к нормальному. Отметим, что при размере выборки n=30, выборочное распределение "почти" нормально.

Статистическая надежность, или уровень вероятности – это площадь под кривой, ограниченная от среднего на t стандартных отклонений, выраженная в процентах от всей площади. Иными словами, это вероятность появления значения признака, лежащего в области μ + t σ. Уровень значимости – это вероятность того, что значение изменяющегося признака находится вне пределов μ + t σ, то есть, уровень значимости указывает вероятность отклонения случайной величины от установленных пределов варьирования. Чем больше уровень вероятности, тем меньше уровень значимости.

В практике агрономических исследований считается возможным пользоваться вероятностями 0,95 – 95% и 0,99 – 99%, которым называют доверительными, то есть такие, которым можно доверять и уверенно пользоваться. Так, при вероятности 0,95 – 95% возможность сделать ошибку 0,05 – 5%, или 1 на 20; при вероятности 0,99 – 99% – соответственно 0,01 – 1%, или 1 на 100.

Аналогичный подход применим и к распределению выборочных средних, так как всякое исследование сводится к сравнению средних величин, подчиняющихся закону нормального распределения. Средняя μ, дисперсия σ² и стандартное отклонение σ – параметры генеральной совокупности при n > ∞. Выборочные наблюдения позволяют получить оценки этих параметров. Для больших выборок (n>20-30, n>100) закономерности нормального распределения объективны для их оценок, то есть в области x ± S находится 68,26%, x ± 2S - 95,46%, x ± 3S – 99,73% всех наблюдений. Средняя арифметическая и стандартное отклонение причисляют к основным характеристикам, при помощи которых задается эмпирическое распределение измерений.