Что такое теоретическая механика

Теоретическая механика - это наука о наиболее общих законах механиче­ского движения и равновесия материальных объектов.

Основные понятия и определения теоретической механики возникли на ос­новании многочисленных опытов и наблюдений над явлениями природы с по­следующим абстрагированием от конкретных условий каждого опыта. В теоре­тической механике пользуются предельными абстракциями: материальная точка и абсолютно твердое тело. Приведенные абстракции позволяют изучать самые общие законы механического движения, что и соответствует основной задаче теоретической механики. Теоретическая механика является основой для изучения таких дисциплин как сопротивление материалов и дета­ли машин.

Курс теоретической механики состоит из трех частей: статики, кинематики и динамики.

Статика – раздел теоретической механики, в котором изучается статическое равновесие материальных тел, находящихся под действием приложенных к ним сил.

Основные понятия статики:

1. Если некоторое тело не перемещается по отношению к другому телу, то говорят, что первое тело находится в состоянии относительного равнове­сия. Тело, по отношению к которому рассматривается равновесие других тел, называется телом отсчета.

2. Любое тело под действием приложенных к нему сил изменяет свои гео­метрические размеры и форму, т.е. деформируется. В теоретической ме­ханике эти деформации не учитываются и рассматриваются только недеформируемые – абсолютно твердые тела. Тело называется абсолютно твердым, если расстояние между его любыми двумя точками остается по­стоянным.

3. 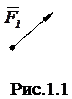Мерой механического взаимодействия тел является сила. Сила – вели­чина векторная, она характеризуется точкой приложения, направлением и модулем (рис. 1.1). Единица измерения силы – нью­тон (Н).

4. Совокупность сил, действующих на какое-либо тело, называется системой сил. Обозначается сис­тема сил { 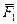, , 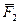, 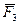… 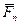} – система, состоящая из n сил.

5. Уравновешенной, или эквивалентной нулю, системой сил называется та­кая система сил, которая, будучи приложенной к твердому телу, не нару­шает его состояния. То есть, если некоторое тело не изменяло свое поло­жение относительно тела отсчета до приложения уравновешенной сис­темы сил, то оно не изменит его и после приложения к нему этой сис­темы. Обозначается уравновешенная система сил так: { 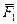, , 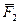, 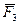… 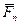}<=>0 (<=> - знак эквивалентности).

6. Если к некоторому телу приложена система сил { 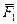, , 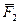, 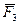… 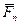} и к нему прикладываем еще одну систему сил { 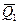, , 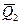, 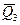… 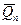}, такую, что вместе с первой она будет составлять уравновешенную систему сил. В этом случае систему { 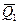, , 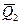, 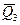… 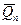}называют уравновешивающей системой сил. Если уравновешивающая система состоит из одной силы 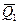, то эта сила называется уравновешивающей силой для системы сил { , , , … }.

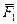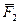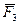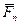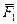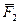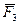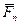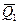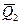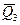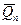7. Если каждая из двух систем сил { , , , … } и { , , , … } уравновешиваются одной и той же системой сил { 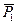, , 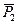, 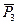… 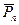}, то первые две системы сил эквивалентны между собой { 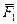, , 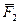, 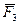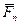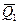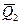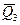… 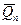} <=>{ , , , … }. Вывод: замена системы сил, действующей на тело, системой ей эквивалентной не изменяет состояния, в котором находится данное тело.

8. Если система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.

Аксиомы статики

Аксиома 1. Свободное абсолютно твердое тело находится в равновесии под действием двух сил, тогда и только тогда, когда силы действуют по одной прямой в противоположные стороны и имеют равные модули.

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней присоединить или от нее отбросить систему сил эквивалентную нулю.

{ , , , … } <=> { , , , … , , , , … };

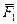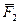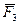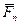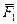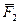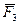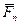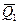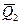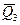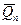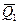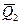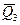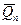{ , , , … } <=> 0

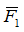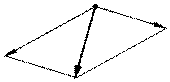
Аксиома 3. Две силы, приложенные в одной точке тела, эквивалентны равнодействующей, приложенной в той же точке и определяемой как диагональ параллелограмма, построенного на силах как на сторонах.

{ , } <=>

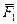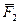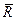
Рис. 1.3

Аксиома 4. Силы взаимодействия двух тел равны по величине и направлены по одной прямой в противоположные стороны.

Тело называется свободным, если его перемещения в пространстве ничем не ограничены. Если на перемещение точек тела накладываются ограничения, то тело называется несвободным или связанным. Материальные тела, ограничивающие перемещения данного тела называются связями. Сила, с которой связь действует на данное тело, называется реакцией связи. Сила действует на связь, а реакция связи на тело.

Аксиома 5. (Аксиома освобождения от связей). Равновесие тела не нарушится, если наложенные на него связи заменить реакциями связей.

Аксиома 6. (Аксиома о затвердевании). Равновесие деформируемого тела не изменится, если на него наложить дополнительные связи или оно станет абсолютно твердым.