Правило эквивалентности прямой последовательности

Из полученных в предыдущих разделах формул для различных видов несимметричных КЗ составим таблицу и проанализируем ее данные (табл. 8.1).

Из таблицы 8.1 видно, что токи обратной и нулевой последовательностей и напряжения всех последовательностей пропорциональны току прямой последовательности в месте КЗ 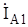. Таким образом, чтобы рассчитать любой вид КЗ, необходимо найти ток прямой последовательности 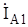в месте несимметричного КЗ.

Периодическую составляющую тока прямой последовательности любой фазы для любого (n) вида несимметричного КЗ можно выразить в общем виде:

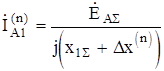, (8.40)

где Dх^{( n)} - дополнительное сопротивление, которое определяется для каждого вида КЗ: Dх⁽³⁾ = 0; Dх⁽²⁾ = х_2S; Dх⁽¹⁾ = х_2S + х_0S;

Dх^(1,1) = х_0S × х_2S / (х_0S + х_2S).

Обобщенная запись выражения (8.40) позволила отечественному ученому Н.Н. Щедрину впервые сформулировать так называемое правило эквивалентности прямой последовательности, которое используется электротехниками всех стран.

Вот его формулировка:

"Ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивление Dх⁽ⁿ⁾ , которое не зависит от параметров схемы прямой последовательности и для каждого вида КЗ определяется результирующими сопротивлениями обратной и нулевой последовательностей относительно рассматриваемой точки схемы..." [2].

Из выражений для напряжения прямой последовательности, приведенных в табл. 8.1 можно записать в общем виде :

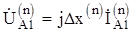. (8.41)

"Установленная идентичность между током прямой последовательности несимметричного КЗ и током при некотором эквивалентном трехфазном КЗ указывает, что все полученные ранее выражения для тока трехфазного КЗ можно распространить на случаи несимметричных коротких замыканий" [2].

Таблица 8.1