Основные формулы и соотношения при несимметричных

Коротких замыканиях

В настоящем разделе рассмотрены три вида несимметричных КЗ (двухфазное - К⁽²⁾, однофазное - К⁽¹⁾ и двухфазное на землю - К^(1,1)). Приводимые выкладки сделаны без учета переходных сопротивлений в месте КЗ (дуга и пр.), то есть все замыкания - металлические. Также данные выкладки приемлемы только для основных гармоник тока и напряжения, а схемы отдельных последовательностей состоят лишь из индуктивных сопротивлений и приведены к элементарному виду относительно точки КЗ, то есть определены результирующая (эквивалентная) ЭДС Е_S и результирующие индуктивные сопротивления прямой x_1S, обратнойx_2S и нулевойx_0S последовательностей. Решение уравнений для каждого вида КЗ выполняется с использованием характеризующих его граничных условий.

При записи граничных условий принимаем, что фаза "А" находится в условиях, отличных от условий для двух других фаз (она называется особой фазой). За положительное направление токов, как фазных, так и их симметричных составляющих, будем считать направление к месту КЗ.

Двухфазное КЗ

Начертим три фазы "А", "В" и "С" для места, где произошло КЗ на незагруженном ответвлении малой длины (сопротивлением этого ответвления можно пренебречь) (рис. 8.7) и запишем граничные условия.

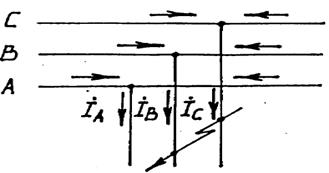
Рис.8.7. Схема для записи граничных условий

Граничные условия: 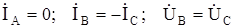. Поскольку двухфазное КЗ не связано с землей, то токи нулевой последовательности протекать не будут, то есть 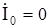. В дальнейших выводах будем использовать формулы метода симметричных составляющих с учетом граничных условий.

Ток в фазе "А" можно записать как 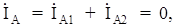откуда

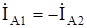.(8.16)

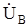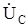Выразим фазные напряжения и через симметричные составляющие фазы "А". Тогда третье граничное условие запишется в следующем виде:

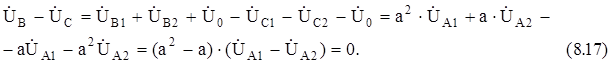
Из выражения (8.17) получим, что

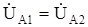. (8.18)

На основании первого и второго уравнений системы (8.13) с учетом (8.16) и (8.18) запишем:

.

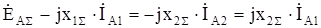Из последнего выражения найдем периодическую составляющую тока прямой последовательности:

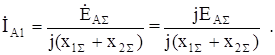(8.19)

Токи в поврежденных фазах "В" и "С" выразим через :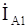

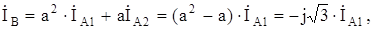(8.20)

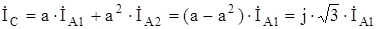.(8.21)

Напряжения прямой и обратной последовательностей фазы "А" в месте КЗ определяются:

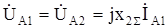. (8.22)

Фазные напряжения в месте КЗ можно определить из следующих выражений:

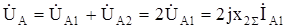, (8.23)

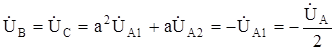. (8.24)

Мы получили выражения токов и напряжений симметричных составляющих для места КЗ, по которым можем строить соответствующие векторные диаграммы. Данные диаграммы приведены на рис. 8.8.

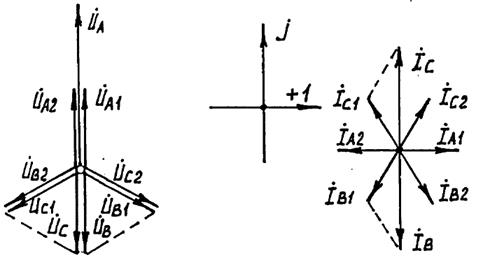
Рис. 8.8. Векторные диаграммы токов и напряжений в месте двухфазного КЗ

Однофазное КЗ

Согласно принципиальной схеме (рис.8.9) для места однофазного КЗ можно записать следующих три граничных условия: .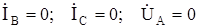

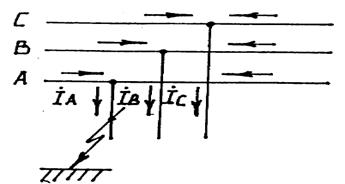
Рис.8.9. Принципиальная схема для места однофазного КЗ

С учетом первого и второго граничных условий можно записать симметричные составляющие токов КЗ:

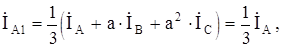
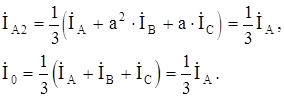
Таким образом,

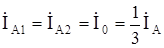. (8.25)

Распишем третье граничное условие через симметричные составляющие и уравнения равновесия напряжений (8.13) для результирующих схем замещения:

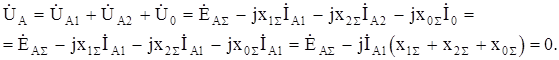
Из последнего выражения получим:

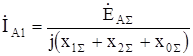. (8.26)

Ток поврежденной фазы в месте КЗ

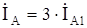. (8.27)

Симметричные составляющие напряжений в месте КЗ:

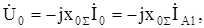(8.28)

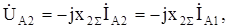(8.29)

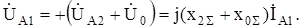(8.30)

Фазные напряжения в месте КЗ:

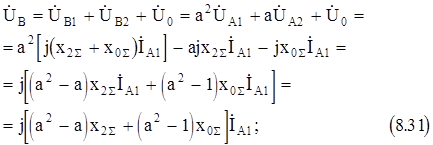
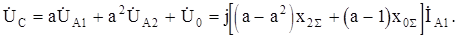(8.32)

По полученным выражениям симметричных составляющих токов и напряжений для места КЗ строим векторные диаграммы (см. рис. 8.10).

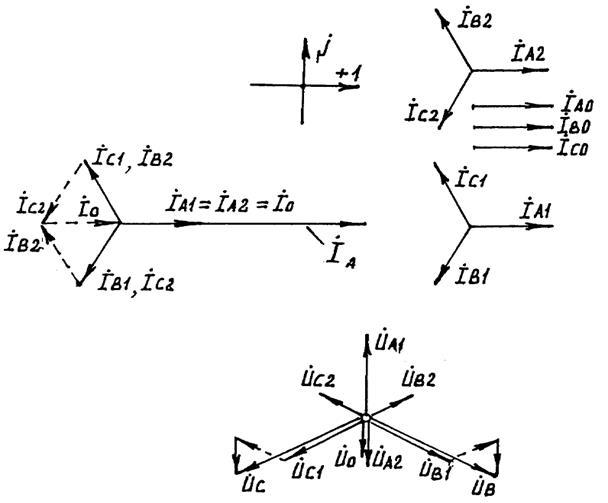
Рис. 8.10. Векторные диаграммы токов и напряжений в месте однофазного КЗ

Угол между векторам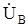и и 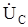зависит от соотношения между x_0S иx_2S. Он изменяется в пределах от 60° до 180°. Нижний предел соответствует x_0S = ¥, а верхний - x_0S = 0. Если x_2S = x_0S,то угол составляет 120°.