Длина тел в разных системах отсчета

Рассмотрим стержень, покоящийся относительно системы К′ (назовем ее собственной системой отсчета)и расположенный вдоль оси х′ . Система К′ движется относительно системы К вдоль оси х со скоростью v =const. Длина стержня в системе К′ равна l₀ = x′₂ - x′_{1 .} Найдем длину стержня в системе К, относительно которой стержень движется со скоростью v. Для этого необходимо зафиксировать координаты концов движущегося стержня х₁ и х₂ в системе К в один и тот же момент времени t₁ = t₂ = b . Применив преобразования Лоренца, получим 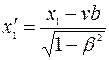и . 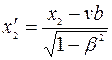Следовательно, длина стержня в системе К равна

l = x₂ – x₁ = (x′₂ − x′₁) 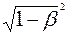= l₀ 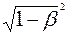. (2.3.8)

Из выражения (2.3.8) следует, что длина стержня, измеренная в системе отсчета, относительно которой он движется, меньше длины, измеренной в собственной системе отсчета, относительно которой стержень покоится, т.е. линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения. Это уменьшение получило название Лоренцова сокращения. Из уравнений (2.3.5) и (2.3.6) преобразований Лоренца следует, что поперечные размеры тела при этом одинаковы во всех инерциальных системах отсчета, т.е. y₂ – y₁ = y′₂ − y′₁; z₂ − z₁ = z′₂ − z′₁. Следует отметить, что такое «сокращение» длины не связано с деформациями самой линейки. Оно обусловлено тем, что одновременная фиксация концов движущегося стержня наблюдателем, находящимся в системе К, является неодновременной в системе К'.