Длительность событий в разных системах отсчета

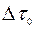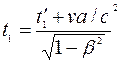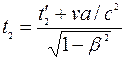Пусть в системе К′ в точке с координатами х′₁ = х′₂ = a происходит событие, которое по часам, покоящимся в системе К′ , начинается в момент времени t′₁ и заканчивается в момент времени t′₂ . Длительность события в системе К′ составляет = t′₂ – t′₁ . Найдем длительность этого события в системе отсчета К . В системе К началу и концу события соответствуют моменты времени и , отсчитанные по часам, покоящимся относительно этой системы. Длительность события в системе К равна

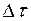= t₂ − t₁ = 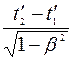= 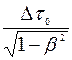. (2.3.9)

Из соотношения (2.3.9) вытекает, что 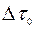< 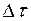, т.е. часы, движущиеся относительно инерциальной системы отсчета

К (часы в системе К′), идут медленнее часов, покоящихся в этой системе. Время 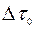, показываемое часами, движущимися вместе с телом (покоящимися относительно тела), называется собственным временем.

Релятивистский эффект замедления времени получил экспериментальное подтверждение в опытах с 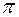- мезонами (нестабильными элементарными частицами). Собственное время жизни заряженных 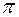- мезонов 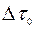= 2,6‧10^-8 с (по часам, покоящимся относительно частицы). Пучок 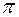-мезонов, выходящий из циклотрона со скоростью 0,75 с, пролетал до полного распада относительно лаборатории расстояние s_лаб= =8,5 ∓ 0,6 м. Если подсчитать расстояние, умножив скорость мезонов на собственное время жизни, то получится, что 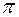-мезоны могли бы пройти относительно лаборатории только расстояние s_π = 0,75с‧2,6‧10^-8 = 5,85 м. Из-за релятивистского замедления времени срок жизни 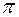-мезона в лабораторной системе отсчета равен

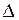
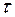_лаб = 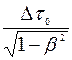= = 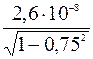3,9∙10^-8 с.

С учетом этого s_лаб=0,75с ∙ 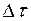_лаб=0,75∙3∙10⁸∙3,9∙10^-8 =8,8 м, что хорошо согласуется с экспериментом и подтверждает теорию.

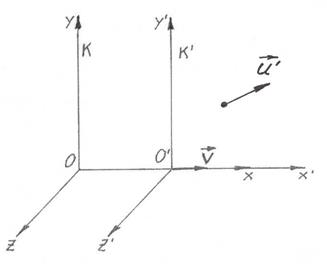
Рис. 2.3.2