ГЛАВА 5. МИНИМАКСНЫЙ ПОДХОД

Минимаксный подход является удобным, а иногда и единственным средством получения правила решения u(х) в тех случаях, когда апри­орная неопределенность распространяется только на распределение ве­роятности параметров l, не наблюдаемых непосредственно, но влияю­щих на последствия от принятия решения. Особенно велико его значение для ситуаций, когда данные наблюдения х не содержат сведений об априорном распределении l. Это имеет место, если эти данные получены для единственного значения l, или еще дополнительно для нескольких известных значений l, но так, что относительная частота различных значений l не связана с распределением p(l). Конечно, мини­максный подход имеет более широкое значение и может применяться и тогда, когда априорная неопределенность распространяется на статис­тическое описание и данных наблюдения х и параметров l, однако ого­воренный выше случай имеет некоторую специфику, которая заслужива­ет отдельного рассмотрения.

Если априорная неопределенность относится только к l (априорное распределение l с плотностью р(l) полностью или частично неизвест­но), то для всякого правила решения u(х) средний риск будет прини­мать различные значения, соответствующие разным р(l) из множества r_о, содержащего все возможные при данном уровне априорной неопре­деленности распределения l. Если к тому же данные наблюдения х не содержат сведений о распределении l, то класс минимаксных правил решений может быть сужен до множества U₀(x) всех байесовых реше­ний, соответствующих всем возможным априорным плотностям вероят­ности р(l)Îr_о. Это утверждение следует из теорем о полноте байесова класса решений и условий их справедливости, которые в данном случае выполняются.

При этом также имеет место равенство минимакса и максимина для риска R(u(х),р), то есть

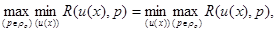(5.1.1)

откуда следует, что отыскание минимаксного правила решения можно свести к процедуре отыскания наименее предпочтительного распределе­ния вероятности с плотностью р(l)Îr_о и последующему нахождению байесова правила решения относительно этого априорного распределе­ния. (Существенно отметить, что в отличие от общего случая (гл. 4) максиминная задача может решаться не относительно общих мер m(р), заданных на множестве r возможных распределений вероятности {P(х|l), р(l)}, а непосредственно относительно р (l), заданных на мно­жестве возможных значений l.).