ИСПОЛЬЗОВАНИЕ ДОСТАТОЧНЫХ СТАТИСТИК

Фактически нахождение правила решения 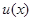, удовлетворяющего одному или сразу нескольким рассмотренным выше принципам пред­почтения, представляет собой далеко не простую задачу. Это связано с тем, что даже задача отыскания байесова правила решения при от­сутствии априорной неопределенности, несмотря на существование об­щих рецептов, подчас оказывается слишком сложной из-за трудностей вычисления апостериорного риска в явной и вполне детализированной форме. В этом отношении большую пользу при решении конкретных задач приносит использование достаточных статистик (минимальных или хотя бы достаточно малой размерности), о которых шла речь в гл. 2. Дело в том, что для практических задач синтеза информационных си­стем характерно наличие большой размерности - в первую очередь, данныхх, описывающих результаты наблюдения, - что существенно затрудняет получение окончательных замкнутых результатов. Использо­вание достаточных статистик резко понижает размерность задачи, что приносит существенное упрощение и при чисто байесовом подходе, а в задачах с априорной неопределенностью часто позволяет получить конкретные алгоритмы принятия решений, основанные только на до­статочных статистиках и являющиеся если не абсолютно оптимальными, то, по крайней мере, обладающие многими чертами оптимальности. Есте­ственно также, что при относительно малой размерности легче выявить условия существования строго или приближенно равномерно наилучше­го правила решения. Даже если эти условия не выполняются или не на­ходятся, то нахождение достаточных статистик способствует отысканию и пониманию структуры оптимального правила решения - функционального соответствия между данными наблюдения х и решением 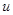.Последнее обстоятельство позволяет целенаправленно и с пониманием существа дела ввести аппроксимацию зависимости 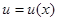, исключить возможные неизвестные параметры, делающие эту зависимость не впол­не определенной, и т. п. Таким образом, можно утверждать, что выяв­ление достаточных статистик малой размерности является если не обя­зательным, то весьма целесообразным элементом решения задачи синтеза в условиях априорной неопределенности.

Общее определение достаточных статистик и правила их нахожде­ния рассмотрены в § 2.6. Из этих результатов следует, в частности, что совокупность величин 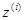(4.2.7) является достаточной статистикой для решения задачи различения сигналов { 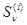}, наблюдаемых в смеси с гауссовой помехой произвольной (в том числе неизвестной) интенсивности. Если дополнить их еще одной величиной 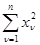, то полученная совокупность будет достаточной статистикой для решения той же зада­чи уже с произвольными вероятностями появления сигналов 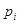и произ­вольной матрицей потерь 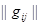, не равными 1/m и 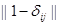соответствен­но, как в § 4.2.

Для задач синтеза в условиях априорной неопределенности особое значение имеют инвариантные достаточные статистики, то есть такие пре­образования 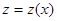, распределения вероятности которых одинаковы при любом распределении вероятности х из класса P_l . Если инвари­антная достаточная статистика существует, то можно ввести такое пре­образование 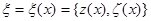, что функция правдоподобия, запи­санная в новых переменных 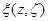, для всех элементов 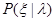класса P_l , соответствующего имеющейся априорной неопределенности, может быть представлена в виде

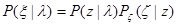, (4.5.1)

где 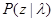- одинакова для всех 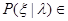P_l . Отсюда немедленно сле­дует, что апостериорное распределение 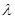одинаково для всех элементов P_l и, следовательно, априорная неопределенность является несущественной. Таким образом, отыскание инвариантной достаточной статистики фак­тически эквивалентно устранению первоначально имевшейся априорном неопределенности.

К сожалению, общие методы отыскания инвариантных или приближенно инвариантных достаточных статистик не разработаны, а сущест­вование строго инвариантных достаточных статистик - довольно редкое явление. Тем не менее, это понятие полезно, поскольку его использо­вание приводит к довольно быстрому решению достаточно сложных за­дач, среди которых выделяются двухальтернативные задачи с так назы­ваемой свободной альтернативой. Этот термин соответствует тому слу­чаю, когда одна из альтернативных ситуаций как-то задана (полностью или частично), а о второй вообще ничего не известно и она может быть совершенно произвольной (естественно, не совпадающей с заданной). Фактически подобные задачи отражают широкий круг практических потребностей, связанных с нахождением правил проверки какого-либо однозначно или многозначно заданного гипотетического предположения, когда альтернативой этому предложению может быть все, что угодно.

Рассмотрим для примера задачу, когда по результатам наблюдения 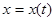в дискретных точках 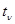( 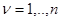) требуется решить, содер­жит ли 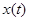сигнал из заданного класса 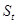или нет. Пусть заданный класс удовлетворяет следующему описанию

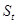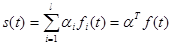: , (4.5.2)

где 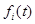- известные функции времени; 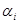- произвольные неизвестные коэффициенты: 1 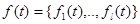, 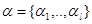- соответствующие векторы (столбцы) неизвестных коэффициентов и известных функций, т - знак транспортирования ( 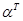- вектор-строка). Данные наблюдения х представляют собой последовательность

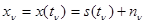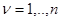, , (4.5.3)

где 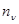- гауссова некоррелированная помеха с дисперсией 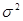и нулевым математическим ожиданием. Альтернативой (4.5.2) может быть со­вершенно произвольный сигнал.

Функция правдоподобия при условии, что 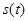принадлежит классу (4.5.2) (будем считать, что этой ситуации соответствует ( 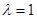), имеет значение

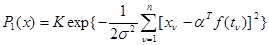(4.5.4)

(К .- несущественный нормировочный множитель) и зависит от сово­купности l неизвестных параметров 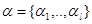. Значение функции правдоподобия для альтернативной ситуации ( 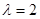) равно

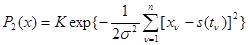, (4.5.5)

где 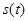- совершенно произвольный сигнал, и фактически вообще не­известно из-за неопределенности этого сигнала. Таким образом, мы име­ем двухальтернативную задачу с весьма большой априорной неопреде­ленностью.

Из-за крайней неопределенности во второй ситуации очевидно, что никакой нетривиальной достаточной статистики, кроме последователь­ности { 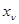}, для этой ситуации не существует. Для первой же ситуации существует весьма экономная (одномерная) достаточная статистика, распределение вероятности которой не зависит от неизвестных парамет­ров 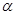, создающих априорную неопределенность в этой ситуации. Действительно, (4.5.4) можно преобразовать к виду

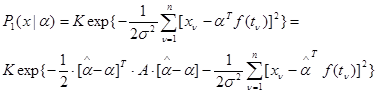, (4.5.6)

где

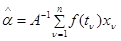(4.5.7)

- оптимальная линейная оценка вектора ;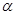

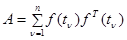(4.5.8)

- положительно определенная матрица порядка { 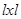}. Нетрудно убе­диться, что распределение вероятности одномерной статистики

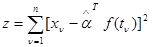(4.5.9)

не зависит от значений неизвестных параметров 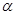, поэтому величина 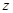из (4.5.9) обладает свойством инвариантности, и всякое правило реше­ния, использующее только эту величину, будет иметь вероятность оши­бочно отвергнуть исходную гипотезу о принадлежности сигнала 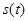классу (4.5.2), одинаковую при любых значениях 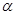, то есть для всех представителей этого класса.

Остальные 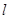статистик 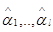, через которые совместно с 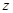выра­жается функция правдоподобия (4.5.6), несут информацию только о зна­чениях неизвестных параметров 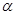, уточняя тем самым вид сигнала 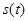в пределах класса (4.5.2). Исходя из этого, а также из полной неопре­деленности для альтернативной ситуации, кажется достаточно правдо­подобным, что оптимальное правило решения о соответствии сигнала 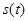, наблюдаемого в смеси с гауссовой помехой, заданному классу (4.5.2) должно использовать только статистику 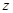из (4.5.9). Разными способами, например, на основе понятия равномерно наиболее мощного критерия для гипотезы со свободной альтернативой, применением минимакса и развиваемыми ниже методами, можно доказать, что эта действительно так, и оптимальное правило принятия решения следую­щее: принимается, что сигнал 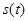принадлежит классу (4.5.2), если

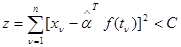, (4.5.10)

где С - некоторый порог сравнения, который определяется из дополни­тельных соображений, например, так, чтобы вероятность ошибочно отвергнуть исходную гипотезу имела заданное значение (в силу инвари­антности статистики 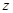одинаковое для всевозможных значений ).

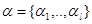Аналогичными свойствами строгой или приближенной инвариант­ности и достаточности обладают статистики, формируемые при использовании известных непараметрических критериев согласия Колмогорова, Смирнова, Мизеса, хи-квадрат и т. д., применяемых в задачах со свободной альтернативой для проверки гипотезы о соответствии данных наблюдения заданному распределению вероятности либо о его неиз­менности для двух совокупностей наблюденных данных. Исследованию свойств этих статистик посвящена обширная литература, поэтому ограничимся только упоминанием о них.

Приведем еще пример, иллюстрирующий свойство достаточных ста­тистик, связанное с возможностью установления структуры правила ре­шения - функциональной зависимости между 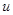и х, о которой шла речь выше. В гл. 2 при обсуждении понятий полного класса решающих пра­вил и достаточной статистики уже приводились некоторые примеры для случая, когда множество решений дискретно. Теперь рассмотрим случай непрерывного множества решений 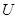, когда требуется оценить значение вектора 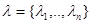по результатам наблюдения вектора 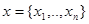, который представляет собой аддитивную смесь с вектором помехи 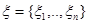. Решение 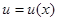является вектором 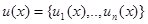, представляющим собой оценку вектора 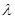. Пусть 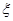и и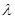меют гауссовы распределения вероятности с корреляционными матрицами (известными либо неизвестным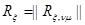и) и 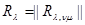соответственно. Тогда плотность совместного распределения вероятности

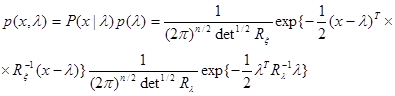, (4.5.11)

где 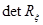- определитель матрицы 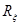; 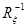- матрица, обратная 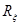(аналогично ).

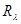Преобразуя выражение (4.5.11), получаем

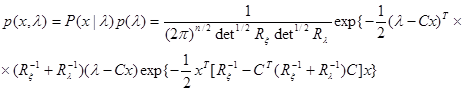(4.5.12)

и апостериорную плотность вероятности

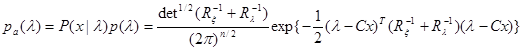, (4.5.13)

где 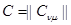– матрица, определяемая из уравнения

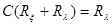. (4.5.14)

Из (4.5.13) следует, что вектор

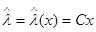, (4.5.15)

представляющий собой линейное преобразование вектора х с матрицей 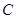из (4.5.14), является достаточной статистикой (поскольку его раз­мерность совпадает с размерностью вектора 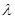, он является также мини­мальной достаточной статистикой). Поэтому всякое оптимальное реше­ние - оценка 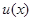вектора 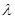для какой-либо функции потерь 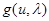- обязательно является функцией только этой достаточной статистики. Фактически, как уже отмечалось в гл. 2, при слабых ограничениях на функцию потерь 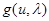оптимальная оценка 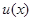совпадает с 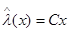из (4.5.15). 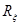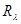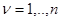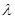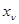Таким образом, если корреляционные матрицы и неизвестны, то есть мы имеем чисто байесову задачу, то нахождение до­статочной статистики (4.5.15) уже означает полное решение задачи син­теза оптимальной процедуры оценивания (фильтрации, если индекс имеет смысл дискретного времени, а и значения под­лежащего выделению и наблюдаемого процессов в дискретные моменты времени). Если же 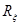и 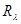полностью или частично неизвестны, то выражение (4.5.15) для достаточной статистики все равно чрезвычайно полезно в том смысле, что устанавливает структуру оптимальной оценки как линейного преобразования вектора х. Это значительно сокращает выбор в условиях априорной неопределенности, поскольку общий вид оптимального алгоритма оценивания ясен и задача заключается только в правильном выборе коэффициентов линейного преобразования (4.5.15).

Некоторые из приведенных выше примеров свидетельствуют о том, что для нахождения байесова правила решения не обязательно тре­буется полное знание распределений вероятности х и 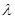, а нечто мень­шее, что дает возможность найти минимум апостериорного риска. Чтобы определить, какие же конкретные сведения об этих распределениях дей­ствительно необходимы для нахождения оптимального правила реше­ния, полезно использовать понятия достаточной статистики. Поясним это на примере. Пусть ставится задача двухальтернативного ре­шения - обнаружения факта наличия сигнала 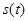по результатам на­блюдения в дискретные моменты времени 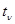его смеси с некоторой не­коррелированной в различные моменты времени помехой. Данные наблюдения представляют собой последовательность 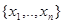, которая может быть порождена либо только одной помехой, либо смесью сиг­нала и помехи. Будем считать, что распределение вероятности помехи и способ ее комбинирования с сигналом произвольны.

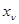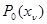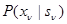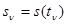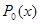В соответствии с этим любая из величин имеет плотность рас­пределения вероятности при отсутствии сигнала и при его наличии, где , а и 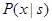- некоторые произвольные плотности вероятности.

Составляя отношение правдоподобия, которое является минималь­ной достаточной статистикой для рассматриваемой двухальтернативной задачи, с учетом независимости значений 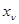получаем

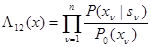. (4.5.16)

Естественно, что в общем случае для реализации оптимального алгорит­ма обнаружения, который состоит в сравнение с порогом 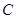отношения правдоподобия, требуется знание функци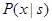й и 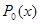, то есть статистики помехи и способа комбинирования сигнала с помехой. Предпо­ложим теперь, что нас интересует часто встречающийся на практике асимптотический случай слабого сигнала. Тогда с учетом равенства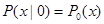

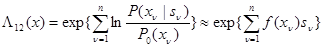, (4.5.17)

где

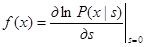. (4.5.18)

Отношение правдоподобия 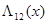является взаимооднозначной функци­ей величины

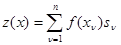, (4.5.19)

которая также является минимальной достаточной статистикой в рас­сматриваемом асимптотическом случае; оптимальный алгоритм обнару­жения заключается в простом сравнении с порогом величины 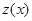. Для реализации этого алгоритма нужно знать лишь первую производную логарифма условной плотности вероятност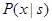и при 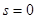, то есть функ­цию 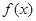из (4.5.18), которая определяет вид нелинейного преобразова­ния наблюдаемых значений 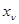. Другие более детальные сведения о виде распределени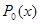й и 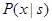для нахождения оптимального алгоритма просто не требуются, поэтому неопределенность, выходящая за пределы знания вида функции 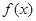, не является существенной.

Аналогично можно рассмотреть большое количество частных, но практически важных задач, однако даже приведенные выше простые примеры достаточно ясно иллюстрируют значение общего подхода, осно­ванного на выделении достаточных статистик и исследовании их струк­туры.