СООТНОШЕНИЯ МЕЖДУ ПРАВИЛАМИ РЕШЕНИЯ, ПОЛУЧЕННЫМИ НА ОСНОВЕ РАЗЛИЧНЫХ ПРИНЦИПОВ ПРЕДПОЧТЕНИЯ

В § 4.3 по ходу рассмотрения уже отмечались некоторые соотноше­ния между правилами решения, следующими из того или иного принци­па предпочтения. Для более полного уяснения их относительного каче­ства рассмотрим ряд дополнительных соотношений. Заметим еще раз, что, конечно, самым хорошим является равномерно наилучшее правило решения, которое при любом 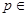P дает такой же риск, как байесово правило решения с известным 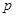. Если равномерно наилучшее правило существует, то оно может быть найдено при использовании любого из рассмотренных принципов предпочтения.

Между минимаксиминным правилом решения 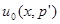и минимакс­ным правилом решения 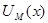существует соотношение

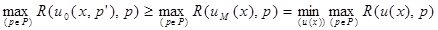, (4.4.1)

которое следует непосредственно из определения этих решений. Соотно­шение между ними показано на рис. 4.4. При 'некоторых 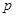риск минимаксиминного правила решения превышает риск минимаксного правила, а при некоторых - имеет меньшие значения.

Аналогичному соотношению удовлетворяет и правило решения 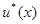, получаемое минимизацией усредненного риска при любой мере :

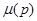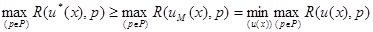. (4.4.2)

Типичное поведение риска 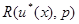по отношению к риску минимакс­ного правила решения 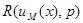в зависимости от 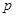показано на рис. 4.4, где приведена также зависимость от 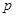минимального байесова риска 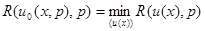, соответствующего известному .

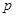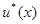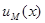В то же время правила решения и удовлетворяют при любой мере 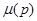соотношению

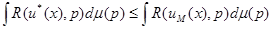, (4.4.3)

которое следует из определения правила решения 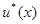. Равенство в (4.4.3) может достигаться только для наименее предпочтительной в со­ответствии с определением (4.3.10) меры 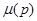. Из соотношений (4.4.2), (4.4.3) следует, что максимум риска по 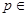P для правила решения 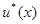не меньше, чем для минимаксного, а усредненное значение риска не боль­ше. Особый интерес представляет слу­чай, когда в (4.4.2) достигается ра­венство, то есть риск правила решения 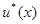не превосходит риска минимаксного правила. При этом очевидно, что правило 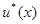равномерно относительно 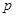лучше (по крайней мере не хуже) минимаксного правила, и следует отдать ему предпочтение. Это обстоятельство является хорошим доводом в пользу принципа минимизации усредненного риска.

Рис. 4.4. Зависимость среднего риска от 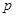для различных правил решения: 1 - байесово; 2 - минимаксное; 3 – минимаксиминное; 4 – минимизации усредненного риска