ПОЛНОЕ НЕЗНАНИЕ АПРИОРНОГО РАСПРЕДЕЛЕНИЯ l

Рассмотрим минимаксное правило решения для случая, когда какие-либо сведения о статистических свойствах l отсутствуют вообще. При этом r_о - множество любых неотрицательных функций, подчиненных условию нормировки на множестве возможных значений l.

Для нахождения минимаксного правила в этом случае полной апри­орной неопределенности относительно l, можно воспользоваться теоремой А. Вальда, согласно которой минимаксное правило решения u_м(х) является байесовым относительно некоторого наименее предпочтитель­ного распределения вероятности с плотностью р*(l) и обладает тем свойством, что величина условного риска r(u_м(х), l) (2.11) для этого решения одинакова при всех значениях l для которых р*(l) отлична от нуля.

Рассмотрим в качестве примера достаточно общий случай, когда множество возможных значений l непрерывно и представляет собой все пространство некоторой произвольной размерности (если l={l₁, ... ... l_n} - n-мерный вектор, то это множество - n-мерное евклидово пространство). Множество решений U также непрерывно и имеет ту же структуру, то есть решение u = u(x) является оценкой l.

Пусть функция потерь g(u, l) имеет вид

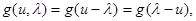(5.2.1)

то есть является симметричной функцией разности u - l₁, и пусть существу­ет такая достаточная статистика z = z(x), для которой плотность рас­пределения вероятности выражается как

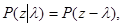(5.2.2)

где Р - симметричная функция своего аргумента. Апостериорный риск для какого-либо произвольного распределения вероятности l с плот­ностью p(l) вычисляется по формуле

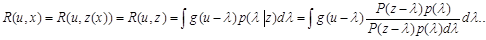(5.2.3)

Предположим теперь, что априорное распределение вероятности l равномерно на всем множестве значений l. Тогда с учетом свойств функций g и Р апостериорный риск

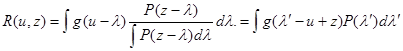. (5.2.4)

Минимум апостериорного риска достигается при u - z = 0, в чем легко убедиться, например, дифференцированием (5.2.4) по компонентам век­тора u. Таким образом, при данном априорном распределении опти­мальное правило решения u(х) имеет вид

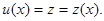(5.2.5)

Найдем условный риск для этого правила. Поскольку u(х) зависит от х только через z = z(x), то

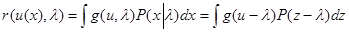. (5.2.6)

или с учетом u(x) = z = z(x)

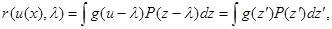(5.2.7)

откуда следует, что условный риск не зависит от l, равномерное рас­пределение l наименее предпочтительно, а правило решения (5.2.5) яв­ляется минимаксным.

С другой стороны, из (5.2.2) следует, что

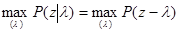(5.2.8)

достигается при l₁ = z, то есть достаточная статистика z = z(x) является оценкой максимального правдоподобия параметра l₁, которая может быть найдена путем максимизации исходной функции правдоподобия P(х|l₁.), то есть из уравнения

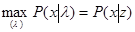, (5.2.9)

которое с точностью до обозначений совпадает с уравнением (2.2.2), при­веденным в гл. 2 в качестве уравнения, определяющего приближенное байесово решение задачи оценки при произвольном невырожденном распределении параметра l и высокой информативности данных наблюдения х относительно l в указанном в гл. 2 смысле. Теперь же мы убедились, что оценка максимального правдоподобия является также ми­нимаксной оценкой для произвольной симметричной функции потерь. Конечно, строго говоря, это имеет место, когда плотность распределения вероятности оценки максимального правдоподобия l* = l*(x) = z(x) имеет вид (5.2.2) (заметим, что это условие слабее, чем предположение о существовании эффективной оценки параметра l, и выполняется в большинстве случаев), однако в действительности оценки максималь­ного правдоподобия обладают минимаксными свойствами в более широ­ких условиях.