Обработка результатов измерений и наблюдений.

Классификация погрешностей:

Погрешность(неопределённость) - отклонение результата измерения Ах от истинного значения А. В международной практике рекомендовано применение термина неопределённость, в отечественной нормативной документации и учебной литературе преобладает использование термина погрешность.

= Ax - A - формула погрешности, где:

A - истинное значение - значение, которое бы идеальным образом отражало в качественном и количественном отношениях измеряемую величину;

Ax – результат измерения. Так как истинное значение величина идеальная и, следовательно, неизвестная, то на практике вместо нее применяют действительное значение A0:

= Ax - A0

A0 - действительное значение, найденное экспериментальным путем и настолько приближающееся к истинному, что для данной цели может быть использовано вместо него.

Классификация погрешностей.

1. по характеру проявления:

1.1 систематические – составляющие погрешности, остающиеся постоянными или закономерно изменяющимися при повторном измерении одного и того же значения;

1.2 случайные – составляющие погрешности, изменяющиеся случайным образом при повторном измерении одного и того же значения;

1.3 грубые – составляющие погрешности, существенно превышающие ожидаемые, при данных условия измерения;

2. по источнику возникновения:

2.1 методические – составляющие погрешности, вызванные несоответствием теоретической модели эксперимента реальному состоянию;

2.2 инструментальная – погрешность применяемых средств измерения;

2.3 субъективная – погрешность, вносимая субъектом, проводящим эксперимент;

3. по условиям применения:

3.1 основная – погрешность средства измерения, применяемые в нормальных условиях;

3.2 дополнительная – погрешность, вызванная отклонением условий измерения от нормальных;

4. по характеру поведения измеряемой величины в процессе измерения:

4.1 статическая – погрешность средства измерения при измерении неизменной в процессе измерения величиныD_стат;

4.2 в динамическом режиме D_{динам.реж.} – погрешность средства измерения при измерении меняющейся во времени в процессе измерения величины;

4.3 динамическая D_динам. = D_{динам.реж.} + D_стат.

5. по закономерности зависимости от размера измеряемой величины:

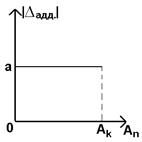
5.1 аддитивные

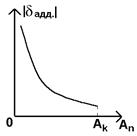
5.2 мультипликативные

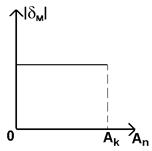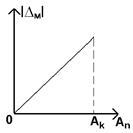
А_п – показания приборов;

А_к – конечное значение диапазона измерения.

6. по способу выражения:

6.1 абсолютная D = А_х – А₀ [ед. измерения]

6.2 относительная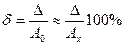

6.3 приведенная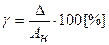

А_н – нормирующее значение (может быть равным конечному значению шкалы, либо – ее геометрической длине либо – диапазону измерения, либо – произвольным).

Относительную погрешность часто выражают в %. Для этого нужно на 100

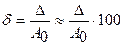
Точность измерений.

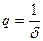
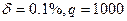
Оценка инструментальной погрешности измерений

Инструментальную погрешность нормируют путем указания пределов допускаемой погрешности, которые указываются в метрологических характеристиках средства измерения.

D_пред. – наибольшая по модулю погрешность средства измерения, при которой оно еще может быть допущено к применению. Фактически, это граница погрешности, за которую она не должна выходить. Таким образом, это позволяет определить границы, в которых находится истинное значение измеряемой величины A:

А_х + D_пред. > А > А_х - D_пред.

Пределы допускаемых погрешностей средств измерений могут быть указаны в метрологических характеристиках в разной форме:

1. в форме абсолютной погрешности: класс точности обозначается M, N, O, R… или I, II, III…

1.1 D_пред. = a;

1.2 D_пред. = (a + вА_к);

1.3 D_пред. = j(А_к),

где (а) и (в) константы, указываемые в метрологических характеристиках,

j(А_к) - может быть задана формулой, отличной от формулы указанной в пункте 1.2, графиком или таблицей;

2. в форме относительной погрешности:

2.1 класс точности обозначен ã, где с число из ряда:

(1; 1,5; 2; 2,5; 4; 5; 5) × 10ⁿ , где n = 1, 0, -1, -2...

d_пред. = c [%]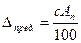

2.2 класс точности обозначен c / d – c и d числа из ряда, указанного в пункте 2.1;

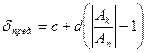
где А_к – наибольший по модулю из диапазонов измерения;

А_n – показания прибора

2.3 если класс точности обозначен, как в пункте 1, то d_пред задается либо формулой, отличной от формулы указанной в пункте 2.2, либо графиком, либо таблицей;

2. в форме приведенной погрешности:

если класс точности обозначен, g - число из ряда, указанного в пункте 1, то

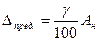
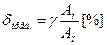, где:

А_н – нормирующее значение, которое может быть равно:

а) А_н = A_к, если нулевая отметка находится на краю шкалы;

б) А_н = |A_k1| + |A_k2|, если нулевая отметка находится внутри рабочей части шкалы;

в) А_н = |A_k1| - |A_k2|, если нулевая отметка находится вне пределов шкалы (приборы с условным нулем), гдеA_к, A_k1 и A_k2 – конечные значения шкалы прибора. При измерении нужно стремится, чтобы показание прибора было как можно ближе к нормирующему значению. Вышеуказанные обозначения применяют для приборов с равномерной шкалой.

3.1 Для приборов с существенно неравномерной шкалой:

Обозначение: g

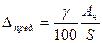
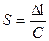
где А_н – нормирующее значение, равное геометрической длине всей шкалы приборов;

S – чувствительность приборов в точке отсчета показания;

Dℓ - размеры одного деления;

С – цена деления.

Случайная составляющая погрешности измерения (СлСПИ)

и ее оценка.

Случайные погрешности исследуют и оценивают с помощью теории вероятности.

СлСПИ – погрешность изменяющаяся случайным образом, которая меняется при повторных измерениях случайным образом.

a₁, a₂, a₃ … a_i … a_n – ряд наблюдений,

n – число наблюдений,

a_i – результат наблюдения (РН),

Случайная погрешность результата наблюдений: D_i = a_i - A

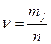, где

m_j – количество наблюдений, погрешность которых попала в j-ый интервал,

n - частота появления события.

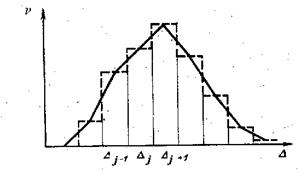
Гистограмма - зависимость частоты появления события от размера события. При предельном переходе гистограмма превращается в дифференциальный закон распределения плотности вероятности (правый график)

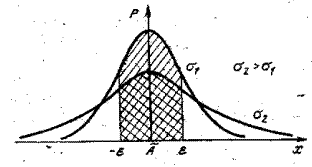
Чаще других встречается нормальный закон распределения случайных погешностей:

,

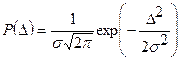где s - среднеквадратическое отклонение (СКО).

Нормальный закон распределения характеризуется двумя параметрами:

математическое ожидание M и среднеквадратическое отклонение s.

Введем новую переменную:

,

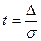которая представляет собой нормированную случайную погрешность. Пусть e граница доверительного интервала случайной составляющей погрешности, тогда 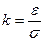– нормированный доверительный интервал этой погрешности. После замены переменных получим следующее выражение

,

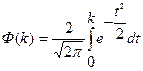которое называют интегралом вероятности. Значение вероятности F(k) приведены в учебниках и математических справочниках