Оценка погрешности косвенных измерений (РД50-555-85)

Пусть существует A = f(a₁, a₂ … a_m), где:

А – величина подвергаемая косвенному измерению,

a₁, a₂ … a_m – измеренные величины (прямые измерения).

1. Исключим СиСПИ из результатов прямых измерений;

2. Найдем 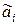, , 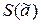Q_i,

где 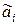- результат I-го измерения,

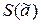- оценка СКО случайной составляющей, Q_I – границы неисключенной систематической составляющей;

3. Проверить степень корреляции аргумента.

Дальнейшая обработка справедлива только для слабо коррелированных величин.

4. 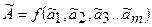- оценка результата косвенного измерения;

5. Вычислить оценку СКО случайной составляющей погрешности результата косвенного измерения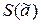

а) ;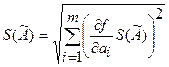

б) если нелинейная зависимость, то 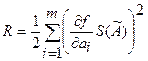, (2);

в) если R ³ 0.8 × 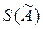, то нужно ввести поправку: ;

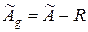6. Вычислить границу неисключенной СиСПРИ

а) если m > 3 и закон распределения равномерный

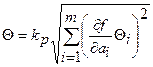, (1);

б) если m £ 3, то рассчитывают по формуле (1) и по формуле 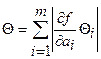, (2)

из двух значений (1) и (2) выбирают меньшее.

Если закон распределения СиСПИ нормальный, то при любом m:

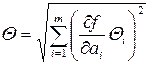, (3).

Все Q_i должны быть определены с одинаковой вероятностью. При P = 0.95, расчет можно вести по любой формуле из (1-3).

Если известны границы суммарной погрешности результатов прямых измерений D_предi, и закон распределения, то для оценки нужно использовать формулу (3), где вместо Q_i ставится D_предi. ДГ суммы погрешностей РИ – см. выше.

Формы представления результатов эксперимента:

1. Результат эксперимента должен быть представлен с указанием единиц измерения;

2. Обязательно должны быть указаны характеристики погрешностей измерения:

2.1 указываются границы суммарной погрешности и доверительная вероятность, с которой погрешность находится в этих границах;

2.2 отдельно указываются характеристики случайной и систематической составляющих погрешности. Причем могут быть указаны либо границы погрешности с указанием вероятности, либо статистические параметры распределения, т.е. оценка СКО и закон распределения (если есть возможность).

3. Погрешность измерения должна выражаться не более чем двумя значащими цифрами.

Можно указать одну значащую цифру, ели погрешность округления не превышает 5 % (погрешность округляют в большую сторону). Если погрешность округления в большую сторону превышает 5%, то можно округлять в меньшую сторону до двух значащих цифр.

4. Критерий округления результата измерения:

последний разряд результата должен быть таким же, как у округленного значения абсолютной погрешности.