ЛЕКЦИЯ 13. ОСТОВНОЕ ДЕРЕВО ГРАФА

Цели и задачи лекции: ознакомить с алгоритмами построения остовных деревьев.

Основные рассматриваемые вопросы: алгоритм Прима, алгоритм Крускала.

Минимальным остовным деревом (МОД) связного взвешенного графа называется его связный подграф, состоящий из всех вершин исходного дерева и некоторых его ребер, причем сумма весов ребер минимально возможная. Если исходный граф несвязен, то описываемую ниже процедуру можно применять поочередно к каждой его компоненте связности, получая тем самым минимальные остовные деревья для этих компонент.
МОД для связного графа можно найти с помощью грубой силы. Поскольку множество ребер МОД является подмножеством в множестве ребер исходного графа, можно просто перебрать все возможные подмножества и найти среди них МОД. Нетрудно видеть, что это чрезвычайно трудоемкий процесс. В множестве из N ребер имеется 2^N подмножеств. Для каждого из этих подмножеств мы должны будем проверить, что оно задает связный подграф, охватывающий все вершины исходного, и не содержит циклов, а затем сосчитать его вес. Процесс можно ускорить после того, как найдено первое остовное дерево. Никакое подмножество ребер, полный вес которого больше, чем у уже найденного наилучшего остовного дерева, не может нам подойти, поэтому нет необходимости проверять связность, ацикличность и охват всех вершин. Однако даже и при этом улучшении сложность метода грубой силы будет порядка O(2^N).

Алгоритм Прима

Воспользуемся для поиска МОД так называемым «алгоритмом ближайшего соседа». В нашем случае мы будем на каждом шаге рассматривать множество ребер, допускающих присоединение к уже построенной части остовного дерева, и выбирать из них ребро с наименьшим весом, проверяя при этом чтобы его присоединение не образовывало циклы. Повторяя эту процедуру, мы получим остовное дерево с наименьшим весом.

Разобьем вершины графа на три класса: вершины, вошедшие в уже построенную часть дерева, вершины, окаймляющие построенную часть, и еще не рассмотренные вершины. Начнем с произвольной вершины графа и включим ее в остовное дерево. Поскольку результатом построения будет некорневое дерево, выбор исходной вершины не влияет на окончательный результат (конечно, если МОД единственно). Все вершины, соединенные с данной, заносим в кайму. Затем выполняется цикл поиска ребра с наименьшим весом, соединяющего уже построенную часть остовного дерева с каймой; это ребро вместе с новой вершиной добавляется в дерево и происходит обновление каймы. После того, как в дерево попадут все вершины, работа будет закончена.
Алгоритм:

выбрать начальный узел

сформировать начальную кайму, состоящую из вершин, соседних с начальным узлом

Цикл пока в графе есть вершины, не попавшие в дерево выполнить:

выбрать ребро из дерева в кайму с наименьшим весом,

добавить конец ребра к дереву,

изменить кайму, для чего добавить в кайму вершины, соседние с новой, включенной,

обновить список ребер из дерева в кайму так, чтобы он состоял из ребер наименьшего веса,

конец цикла.

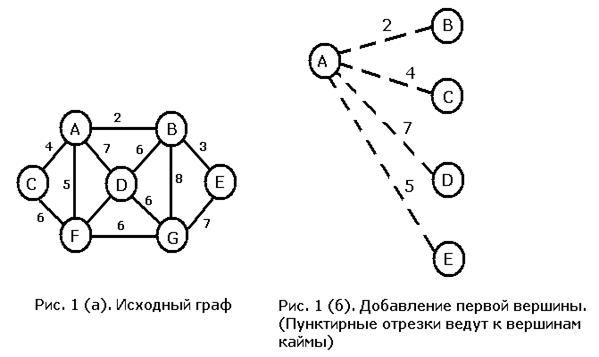
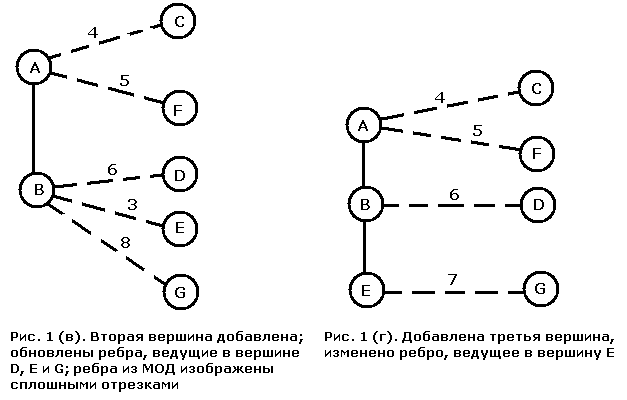
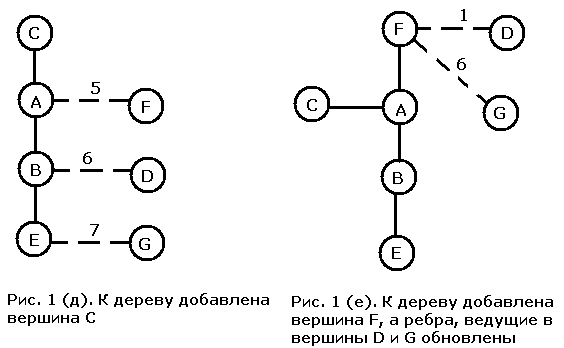
Исходный граф изображен на рис. 1 (а), начинаем построение МОД с вершины A. Все вершины, непосредственно связанные с A, образуют исходную кайму. Видно, что ребро наименьшего веса связывает узлы A и B, поэтому к уже построенной части МОД добавляется вершина B вместе с ребром AB. При добавлении к дереву вершины B (рис. 1 (в)) нужно определить, не следует ли добавить к кайме новые вершины. В результате мы обнаруживаем, что это необходимо проделать с вершинами E и G. Поскольку обе эти вершины соединены только с вершиной B уже построенной части дерева, мы добавляем соединяющие ребра к списку рассматриваемых на следующем шаге. Здесь же необходимо проверить, являются ли ребра, ведущие из вершины A в C, D и F, кратчайшими среди ребер, соединяющих эти вершины с деревом, или есть более удобные ребра, исходящие из B. В исходном графе вершина B не соединена непосредственно ни с C, ни с F, поэтому для них ничего не меняется. А вот ребро BD короче ребра AD, и поэтому должно его заменить. Наименьший вес из пяти ребер, идущих в кайму, имеет ребро BE, поэтому к дереву нужно добавить его и вершину E (рис. 1 (г)). Вес ребра EG меньше веса ребра BG, поэтому оно замещает последнее. Из четырех ребер, ведущих в кайму, наименьший вес имеет AC, поэтому следующим к дереву добавляется оно. Добавление к остовному дереву вершины C и ребра AC (рис. 1 (д)) не приводит к изменению списка ребер.
Затем мы выбираем ребро AF и добавляем его к дереву вместе с вершиной F. Кроме того, мы меняем список связей, поскольку вес ребра FD меньше веса ребра BD, а вес ребра FG меньше веса ребра EG. В получившейся кайме (рис. 1 (е)) ребро FD имеет наименьший вес среди оставшихся, и оно добавляется следующим.
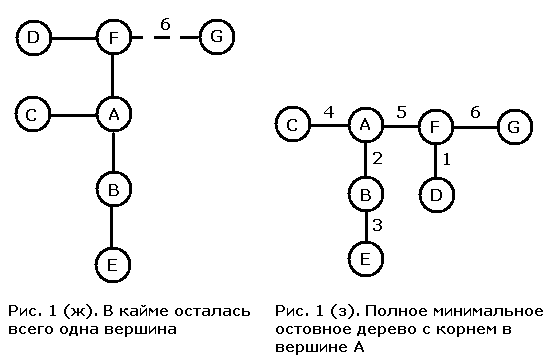
Теперь осталось добавить к дереву всего один узел (рис. 1 (ж)). После этого процесс завершается, и мы построили МОД с корнем в вершине A (рис. 1 (з)).

Алгоритм Крускала
Алгоритм Дейкстры-Прима начинает построение МОД с конкретной вершины графа и постепенно расширяет построенную часть дерева; в отличие от него алгоритм Крускаладелает упор на ребрах графа.
В этом алгоритме мы начинаем с пустого дерева и добавляем к нему ребра в порядке возрастания их весов пока не получим набор ребер, объединяющий все вершины графа. Если ребра закончатся до того, как все вершины будут соединены между собой, то это означает, что исходный граф был несвязным, и полученный нами результат представляет собой объединение МОД всех его компонент связности.
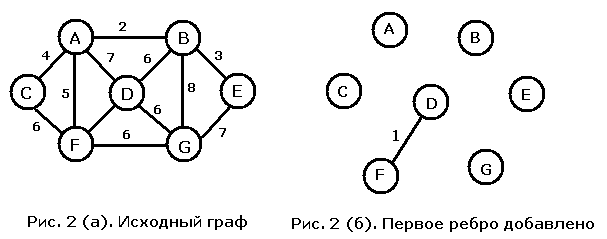
Мы работаем с тем же графом (см. рис. 2 (а)), что и при описании алгоритма Дейкстры -Прима. Начнем с ребра наименьшего веса, то есть с ребра DF. Начальная ситуация изображена на рис. 2 (б).
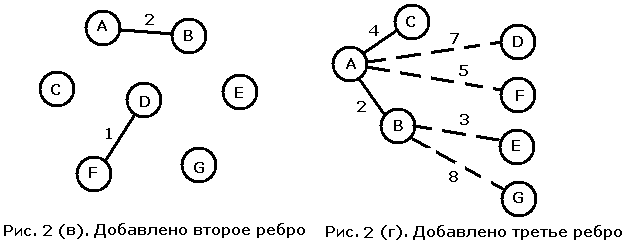
Следующим добавляется ребро веса 2, соединяющее вершины A и B (рис. 2 (в)), а затем - ребро веса три, и мы получаем ситуацию с рис. 2 (г).
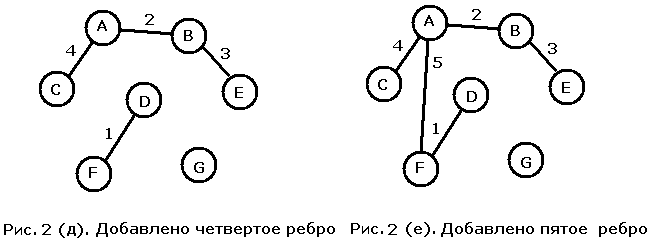
К результирующему графу последовательно добавляются ребра весов 4 и 5 (рисунки 2 (д) и (е)). Несоединенной осталась лишь вершина G. Следующими мы должны рассмотреть ребра веса 6.
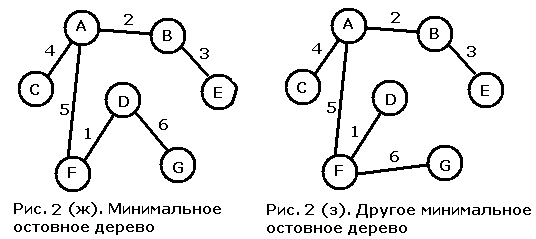
Два из четырех ребер веса 6 следует отбросить, поскольку их добавление приведет к появлению цикла в уже построенной части МОД. Присоединение ребра CF создало бы цикл, содержащий вершину A, а присоединение ребра BD - цикл, содержащий вершины A и F. Обе оставшиеся возможности подходят в равной степени, и, выбирая одну из них, мы получаем либо МОД с рис. 2 (ж), либо МОД с рис. 2 (з).

Сложность этого алгоритма совпадает со сложностью используемого алгоритма сортировки, поскольку число операций в цикле while линейно по числу ребер. Поэтому сложность алгоритма Крускала поиска МОД равна O(Е log Е).