Метод середины квадрата

Первым алгоритмический метод получения равномерно распределенных псевдослучайных чисел предложил Джон фон Нейман (один из основоположников кибернетики). Метод получил название "метод середины квадрата" .

Суть метода: предыдущее случайное число возводится в квадрат, а затем из результата извлекаются средние цифры.

Недостатки метода:

1. Если какой-нибудь член последовательности окажется равным нулю, то все последующие члены также будут нулями.

2. Последовательности имеют тенденцию "зацикливаться", т. е. в конце концов, образуют цикл, который повторяется бесконечное число раз.

Свойство "зацикливаться" присуще всем последовательностям, построенным по рекуррентной формуле Х_i+1=f(xi).

Повторяющийся цикл называется периодом. Длина периода у различных последовательностей разная. Чем больше, тем лучше.

Линейный конгруэнтный метод

Предложен в 1948 году Д.Х.Лемером.

Суть метода: Выбираем четыре числа:

Х₀– начальное значение,Х₀ >= 0;

a – множитель, a>= 0;

c– приращение, c>= 0;

m – модуль, m > x_0, m > a, m > c.

Тогда искомая последовательность случайных чисел получается из соотношения:
Х_i+1=(ax_i+c) Mod(m), n>=0,

т. е. каждое случайное число – это остаток, при делении (axi+c) на m.

Последовательность, полученная из этого соотношения называется линейной конгруэнтной последовательностью.

Однако магические числа не надо выбирать произвольно, так как при некоторых числах последовательность зацикливается.

Проведено много исследований и доказано теорем по вопросу "как правильно выбирать" "магические числа".

Метод получения случайных чисел при c=0 называется "мультипликативный конгруэнтный метод", при c<>0 - "смешанный конгруэнтный метод". При c=0, выработка последовательностей происходит быстрее, но при этом уменьшается длина периода последовательностей.

Выбор модуля m. Для получения длинных последовательностей и для увеличения скорости вычисления рекомендуется m выбирать равным размеру машинного слова.

Значение множителя также влияет на длину периода последовательностей. Известен квадратичный метод, метод получения случайных чисел, где реализуется последовательность Фибоначчи, аддитивные методы, где не требуются операции умножения и деления, и другие методы.

Метод Монте-Карло

Сущность метода Монте-Карло состоит в следующем: требуется найти значение А некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно А:

М(Х) =а.

Практически же поступают так: производят п испытаний, в результате которых получают п возможных значений X, вычисляют их среднее арифметическое и принимают его в качестве оценки (приближенного значения) а* искомого числа а.

Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний.

Отыскание возможных значений случайной величины Х (моделирование) называют «разыгрыванием случайной величины».

Рассмотрим пример, иллюстрирующий метод статистических испытаний:

Система контроля качества продукции состоит из трех приборов. Вероятность безотказной работы каждого из них в течение времени Т равна 5/6. Приборы выходят из строя независимо друг от друга. При отказе хотя бы одного прибора вся система перестает работать. Найти вероятность Ротк того, что система откажет за время Т.

Решим задачу аналитически и методом статистических испытаний.

Аналитическое решение. Событие А (выход из строя хотя бы одного из трех приборов за время Т) и событие А (ни один из трех приборов не выйдет из строя за время Т) - противоположные. Вероятность Р (А) =(5/6)³. Искомая вероятность

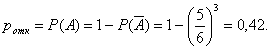
Теперь решим задачу методом статистических испытаний. Напомним, что при использовании данного метода возможны два подхода: либо непосредственно проводят эксперименты, либо имитируют их другими экспериментами, имеющими с исходными одинаковую вероятностную структуру. В условиях данной задачи «натуральный» эксперимент- наблюдение за работой системы в течение времени Т. Многократное повторение этого эксперимента может оказаться трудноосуществимым или просто невозможным. Заменим этот эксперимент другим.

Для определения того, выйдет или не выйдет из строя за время Т отдельный прибор, будем подбрасывать игральную кость. Если выпадет одно очко, то будем считать, что прибор вышел из строя; если два, три, ..., шесть очков, то будем считать, что прибор работал безотказно. Вероятность того, что выпадет одно очко, так же как и вероятность выхода прибора из строя, равна 1/6, а вероятность того, что выпадет любое другое число очков, как и вероятность безотказной работы прибора, равна 5/6.

Чтобы определить, откажет или нет вся система за время Т, будем подбрасывать три игральные кости (или одну кость три раза). Если хотя бы на одной из трех костей выпадет одно очко, то это будет означать, что система отказала.

Повторим испытание, состоящее в подбрасывании трех игральных костей, много раз подряд и найдем отношение числа т «отказов» системы к общему числу п проведенных испытаний. Вероятность отказа

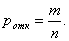
Ранее было указано, что метод Монте- Карло основан на применении случайных чисел; дадим определение этих чисел. Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале (0, 1).

Случайными числами называют возможные значения r_j непрерывной случайной величины R, распределенной равномерно в интервале (О, 1).

В действительности пользуются не равномерно распределенной случайной величиной R, возможные значения которой имеют бесконечное число десятичных знаков, а квазиравномерной случайной величиной R*, возможные значения которой имеют конечное число знаков. В результате замены R на R* разыгрываемая величина имеет не точно, а приближенно заданное распределение.

Случайная величина R* обладает свойством: вероятность попадания ее в любой интервал, принадлежащий интервалу (0; 1) равна длине этого интервала.