Включение в АВЛ-дерево
После включения нового узла в АВЛ-дерево оно должно оставаться сбалансированным. Рассмотрим, в каких случаях потребуется балансировка дерева после включения узла. Во всех случаях будем указывать показатель сбалансированности корневого узла
| До включения (дерево АВЛ-сбалансировано) | После включения | |||||||
| В левое поддерево | В правое поддерево | |||||||
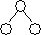 hR = hL hR-hL= 0 hR = hL hR-hL= 0
|
критерий сбалансированности не нарушен |
критерий сбалансированности не нарушен | ||||||
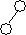 hR < hL hR-hL= -1 hR < hL hR-hL= -1
|
критерий сбалансированности нарушен, нужна балансировка | 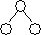 hR = hL hR-hL= 0 критерий сбалансированностине нарушен hR = hL hR-hL= 0 критерий сбалансированностине нарушен
| ||||||
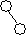 hR > hL hR-hL= 1 hR > hL hR-hL= 1
| 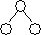 hR = hL hR-hL= 0 критерий сбалансированностине нарушен hR = hL hR-hL= 0 критерий сбалансированностине нарушен
|
критерий сбалансированности нарушен, нужна балансировка |
Таким образом, есть 4 варианта нарушения балансировки:
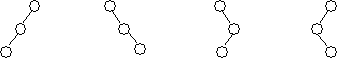
Балансировка выполняется с помощью действий, называемых поворотами узлов. Рассмотрим алгоритмы поворотов, используя указатели p, p1, p2 и считая, что p указывает на узел с нарушенной балансировкой.
Одинарный LL-поворот. Выполняется, когда <перевес> идет по пути L-L от узла с нарушенной балансировкой.
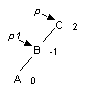
| -> | 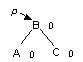
|
p1 := p^.llink;
p^.llink := p1^.rlink;
p1^.rlink := p;
p := p1;
Одинарный RR-поворот.Выполняется, когда <перевес> идет по пути R-R от узла с нарушенной балансировкой.
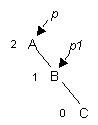
| -> | 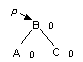
|
p1 := p^.rlink;
p^.rlink := p1^.llink;
p1^.llink := p;
p := p1;
Двойной LR-поворот.Выполняется, когда <перевес> идет по пути L-R от узла с нарушенной балансировкой.
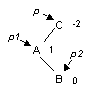
| -> | 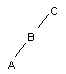
| -> | 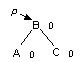
|
p1 := p^.llink;
p2 := p1^.rlink;
p1^.rlink := p2^.llink;
p2^.llink := p1;
p^.llink := p2^.rlink;
p2^.rlink := p;
p := p2;
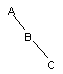
Двойной RL-поворот. Выполняется, когда <перевес> идет по пути R-L от узла с нарушенной балансировкой.
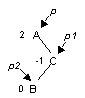
| -> | 
| -> | 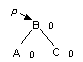
|
p1 := p^.rlink;
p2 := p1^.llink;
p1^.llink := p2^.rlink;
p2^.rlink := p1;
p^.rlink := p2^.llink;
p2^.llink := p;
p := p2;
При включении узлов повороты выполняются для ближайшего узла к включенному с нарушенной балансировкой. То есть если после включения узла в дереве образуется несколько узлов с нарушенной балансировкой, поворот выполняется для того, который находится ниже (то есть ближе к включенному). После балансировки этого узла восстанавливается баланс и выше расположенных узлов.
В качестве примера рассмотрим диаграмму роста АВЛ-дерева поиска, получающегося из последовательности значений 4, 5, 7, 2, 1, 3, 6 (будем указывать тип применяемых поворотов и показатель сбалансированности у узлов с нарушенным балансом):
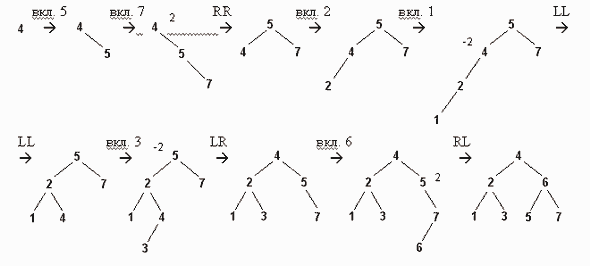
Ясно, что включение узла в АВЛ-дерево в среднем требует больше времени, чем включение в обычное дерево, так как может возникать необходимость проведения балансировки. Поэтому АВЛ-деревья целесообразно использовать в тех случаях, когда поиск узлов в дереве происходит гораздо чаще, чем включение и исключение улов.
Процедура включения в АВЛ-дерево.Для облегчения балансировки при включении узлов будем хранить показатель балансировки в каждом узле:
type ptr = ^node;
node = record
info : integer;
bal : integer;
llink, rlink : ptr;
end;
Дата добавления: 2018-05-10; просмотров: 1425;