Процедура поиска в глубину
Поиск в глубину - вероятно, наиболее важная ввиду многочисленности приложений стратегия обхода графа. Идея этого метода - идти вперед в неисследованную область, пока это возможно, если же вокруг все исследовано, отступить на шаг назад и искать новые возможности для продвижения вперед. Метод поиска в глубину известен под разными названиями, например, "бэктрекинг", "поиск с возвращением".
Понятия новой, открытой, закрытой и активной вершин для поиска в глубину имеют такой же смысл, как и для поиска в ширину. Отметим, что всегда имеется не более чем одна активная вершина.
Обход начинается с посещения заданной стартовой вершины 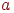 , которая становится активной и единственной открытой вершиной. Затем выбирается инцидентное вершине
, которая становится активной и единственной открытой вершиной. Затем выбирается инцидентное вершине 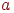 ребро
ребро 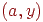 и посещается вершина
и посещается вершина 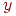 . Она становится открытой и активной. Заметим, что при поиске в ширину вершина
. Она становится открытой и активной. Заметим, что при поиске в ширину вершина 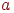 оставалась активной до тех пор, пока не были исследованы все инцидентные ей ребра. В дальнейшем, как и при поиске в ширину, каждый очередной шаг начинается с выбора активной вершины из множества открытых вершин. Если все ребра, инцидентные активной вершине
оставалась активной до тех пор, пока не были исследованы все инцидентные ей ребра. В дальнейшем, как и при поиске в ширину, каждый очередной шаг начинается с выбора активной вершины из множества открытых вершин. Если все ребра, инцидентные активной вершине 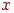 , уже исследованы, она превращается в закрытую. В противном случае выбирается одно из неисследованных ребер
, уже исследованы, она превращается в закрытую. В противном случае выбирается одно из неисследованных ребер 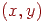 , это ребро исследуется. Если вершина
, это ребро исследуется. Если вершина 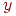 новая, то она посещается и превращается в открытую.
новая, то она посещается и превращается в открытую.
Главное отличие от поиска в ширину состоит в том, что при поиске в глубину в качестве активной выбирается та из открытых вершин, которая была посещена последней. Для реализации такого правила выбора наиболее удобной структурой хранения множества открытых вершин является стек: открываемые вершины складываются в стек в том порядке, в каком они открываются, а в качестве активной выбирается последняя вершина. Схематически это показано на рис. 2.
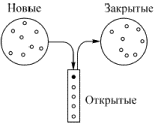
Рис. 2.
Обозначим стек для открытых вершин через 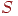 , остальные обозначения сохраняют тот же смысл, что и в предыдущем разделе. Через
, остальные обозначения сохраняют тот же смысл, что и в предыдущем разделе. Через 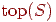 обозначается верхний элемент стека (т.е. последний элемент, добавленный к стеку). Тогда процедура обхода одной компоненты связности методом поиска в глубину со стартовой вершиной
обозначается верхний элемент стека (т.е. последний элемент, добавленный к стеку). Тогда процедура обхода одной компоненты связности методом поиска в глубину со стартовой вершиной 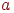 может быть записана следующим образом (DFS - Depth First Search).
может быть записана следующим образом (DFS - Depth First Search).
Procedure DFS(a)
1.посетить вершину 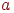
2. 
3.while 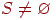 do
do
4. 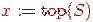
5.if имеется неисследованное ребро 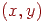
6.then исследовать ребро 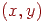
7.if вершина 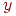 новая
новая
8.then посетить вершину 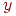
9. 
10. else удалить 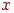 из
из 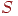
Еще раз обратим внимание на основное отличие этой процедуры от аналогичной процедуры поиска в ширину. При поиске в ширину вершина, став активной, остается ею, пока не будет полностью исследована ее окрестность, после чего она становится закрытой. При поиске в глубину, если в окрестности активной вершины 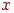 обнаруживается новая вершина
обнаруживается новая вершина 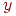 , то
, то 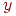 помещается в стек и при следующем повторении цикла while станет активной. При этом
помещается в стек и при следующем повторении цикла while станет активной. При этом 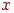 остается в стеке и через какое-то время снова станет активной. Иначе говоря, ребра, инцидентные вершине
остается в стеке и через какое-то время снова станет активной. Иначе говоря, ребра, инцидентные вершине 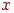 , будут исследованы не подряд, а с перерывами.
, будут исследованы не подряд, а с перерывами.
Алгоритм обхода всего графа - тот же, что и в случае поиска в ширину, только нужно очередь заменить стеком, а процедуру BFS - процедурой DFS.
Свойства 1 и 2 поиска в ширину, отмеченные в предыдущем разделе, сохраняются и для поиска в глубину. Остается верной и оценка трудоемкости 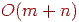 , но ее доказательство требует несколько иных рассуждений, так как каждая вершина теперь может становиться активной несколько раз. Однако каждое ребро рассматривается только два раза (один раз для каждой инцидентной ему вершины), поэтому в операторе if в строке 5 ветвь then (строки 6-9) повторяется
, но ее доказательство требует несколько иных рассуждений, так как каждая вершина теперь может становиться активной несколько раз. Однако каждое ребро рассматривается только два раза (один раз для каждой инцидентной ему вершины), поэтому в операторе if в строке 5 ветвь then (строки 6-9) повторяется 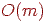 раз. В этом же операторе ветвь else (строка 10) повторяется
раз. В этом же операторе ветвь else (строка 10) повторяется 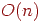 раз, так как каждая вершина может быть удалена из стека только один раз. В целом получается
раз, так как каждая вершина может быть удалена из стека только один раз. В целом получается 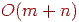 .
.
Дата добавления: 2018-05-10; просмотров: 1398;











