ЛЕКЦИЯ 13. МАТРИЦЫ ПУТЕЙ, ПРОВЕРКА СВЯЗНОСТИ

Цели и задачи лекции: ознакомиться с алгоритмами построения матрицы путей, проверка связност графа..

Основные рассматриваемые вопросы:матрицы путей, проверка связности.

В некоторых матричных алгоритмах обработки графов используются так называемые матрицы путей. Определим понятие пути в ориентированном графе. Под путем длиной k из вершины i в вершину j мы будем понимать возможность попасть из вершины i в вершину j за k переходов, каждому из которых соответствует одна дуга. Одна матрица путей m _k содержит сведения о наличии всех путей одной длины k в графе. Единичное значение в позиции (i,j) означает наличие пути длины k из вершины i в вершину j.

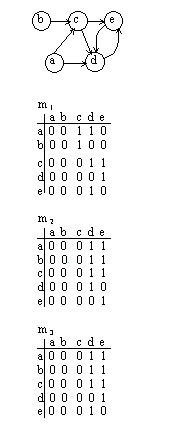
Матрица m₁ полностью совпадает с матрицей смежности. По матрице m ₁ можно построить m ₂ . По матрице m ₂ можно построить m ₃ и т. д. Если граф является ациклическим, то число мариц путей ограничено. В противном случае матрицы будут повторяться до бесконечности с некоторым периодом, связанным с длиной циклов. Матрицы путей не имеет смысла вычислять до бесконечности. Достаточно остановиться в случае повторения матриц.

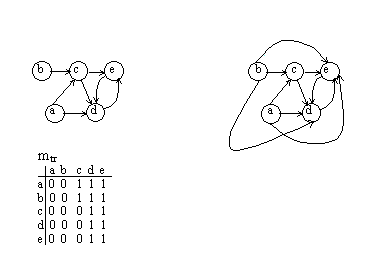
Если выполнить логическое сложение всех матриц путей, то получится транзитивное замыкание графа.

M _tr = m ₁ OR m ₂ OR m ₃

В результате матрица будет содержать все возможные пути в графе.

Наличие циклов

Наличие циклов в графе можно определить с помощью эффективного алгоритма. Алгоритм может быть реализован как для матричного, так и для спискового способа представления графа.

Принцип выделения циклов следующий. Если вершина имеет только входные или только выходные дуги, то она явно не входит ни в один цикл. Можно удалить все такие вершины из графа вместе со связанными с ними дугами. В результате появятся новые вершины, имеющие только входные или выходные дуги. Они также удаляются. Итерации повторяются до тех пор, пока граф не перестанет изменяться. Отсутствие изменений свидетельствует об отсутствии циклов, если все вершины были удалены. Все оставшиеся вершины обязательно принадлежат циклам.

Сформулируем алгоритм в матричном виде

1.Для iот 1 до n выполнить шаги 1-2

2.Если строка M(i ,*) = 0, то обнулить столбец i

3.Если столбец M(*, i) = 0, то обнулить строку i

4.Если матрица изменилась, то выполнить шаг 1

5.Если матрица нулевая, то стоп, граф ациклический, иначе матрица содержит вершины, входящие в циклы

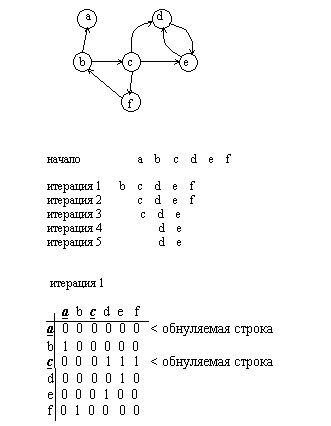
Достоинством данного алгоритма является то, что происходит одновременное определение цикличности или ацикличности графа и формирование списка вершин, входящих в циклы. В матричной реализации после завершения алгоритма остается матрица, соответствующая подграфу, содержащему все циклы исходного графа.

Язык графов оказывается удобным для описания многих физических, технических, экономических, биологических, социальных и других систем. Основные алгоритмы для работы с графами рассмотрим в разделе «Алгоритмы на сетях и графах».