ЛЕКЦИЯ 12. ГРАФЫ ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. СПОСОБЫ ЗАДАНИЯ И РЕАЛИЗАЦИЯ
Цели и задачи лекции: показать способы задания и реализация графов
Основные рассматриваемые вопросы. Основные определения. Способы задания и реализация графов. Наличие циклов, связность.
Граф G - это упорядоченная пара (V, Е), где V- непустое множество вершин, Е - множество пар элементов множества V, называемое множеством ребер.
Упорядоченная пара элементов из V называется дугой. Если все пары в Е упорядочены, то граф называется ориентированным (орграфом).
Если дуга е ведет от вершины vl к вершине v2, то говорят, что дуга е инцидентна вершине v2, а вершина v2 являются смежной вершине vv В случае неориентированного графа ребро е является инцидентной обеим вершинам vl и v2, а сами вершины - взаимно смежными.
Путь - это любая последовательность вершин орграфа такая, что в этой последовательности вершина в может следовать за вершиной а, только если существует дуга, следующая из а в в .
Путь, начинающийся и заканчивающийся в одной и той же вершине, называется циклом. Граф, в котором отсутствуют циклы, называется ациклическим.
Петля - дуга, соединяющая некоторую вершину сама с собой.
- Выбор структуры данных для хранения графа в памяти имеет принципиальное значение при разработке эффективных алгоритмов.
При дальнейшем изложении будем предполагать, что вершины графа обозначены символьной строкой и всего их до п, а ребер - до т. Каждое ребро и каждая вершина имеют вес - целое положительное число. Если граф не является помеченным, то считается, что вес равен единице.
Матрица смежности - это двумерный массив V, размером пХп:
При этом vij=0, если вершина i не смежна вершине; vij=весу ребра (дуги), если вершина i смежна вершине j, vij=весу петли.
Пространственная сложность этого способа V(n)~O(n2). Способ очень хорош, когда надо часто проверять смежность или находить вес ребра по двум заданным вершинам.
Матрица инцидентности — это двумерный массив U размером пХт:
При этом uij=0, если вершина i не инцидентна ребру j, uij=весу ребра, если вершина инцидентна ребру j.
Пространственная сложность этого способа V(n, m)~O(n*m). Матрица инцидентности лучше всего подходит для операции «перечисление ребер, инцидентных вершине х».
Списки смежных вершин - это одномерный массив размером п, содержащий для каждой вершины указатели на списки смежных с ней вершин:
type
PNode = ANode;
Node = record {смежная вершина}
Name: string; {имя смежной вершины}
Weight: integer; {вес ребра}
Next: PNode; {следующая смежная вершина}
end;
TAdjacencyList = array [l..n] of record
NodeWeight: integer; {вес вершины}
Name: string; {имя вершины}
List: PNode; {указатель на список смежных}
end; var
Graph: TAdjacencyList;
Пространственная сложность этого способа Fmax(w)~0(w2). Хранение списков в динамической памяти позволяет сократить объем расходуемой памяти, так как в этом случае не будет резервироваться место под п соседей для каждой вершины. Можно и сам массив представить в виде динамического списка, но это не имеет особого смысла, так как граф обычно является статичной (неизменяемой) структурой.
Этот способ хранения лучше всех других подходит для операции «перечисление всех вершин, смежных с х».
Список ребер - это одномерный массив размером т, содержащий список пар вершин, инцидентных с одним ребром графа:
Пространственная сложность этого способа V(m)~O(m). Этот способ хранения графа особенно удобен, если главная операция, которой чаще всего выполняется, это перечисление ребер или нахождение вершин и ребер, находящихся в отношениях инцидентности.
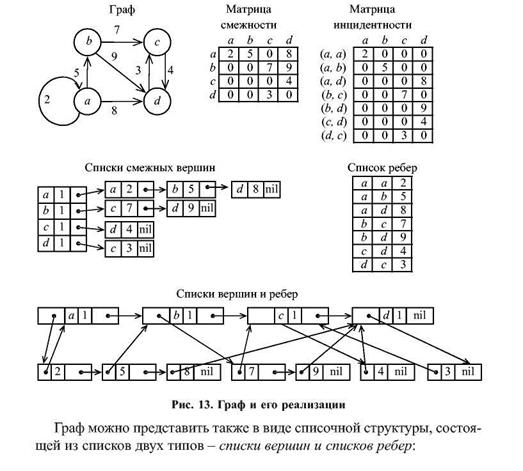
type
PNode = ATNode;
PBranch = ATBranch;
TNode = record {вершина}
Name: string; {имя вершины}
Weight: integer; {вес вершины}
Branch: PBranch; {выходящее ребро}
Next: PNode; {следующая вершина} end; TBranch = record {ребро}
Node: PNode; {вершина, в которую входит}
Weight: integer; {вес ребра}
Next: PBranch; {следующее выходящее ребро} end; var
Graph: PBranch;
Пространственная сложность этого способа V(n, m)~O(n+m).
Дата добавления: 2018-05-10; просмотров: 1794;











