Взаимодействие электромагнитных волн с веществом

Электромагнитные волны способны распространяться не толь­ко в вакууме, но и в различных средах, т. е. в веществе. При этом претерпевает изменения и характеристики излучения, и характеристики вещества. Рассмотрим вкратце основанный' на пред­ставлениях классической физики механизм взаимодействия электромагнитной волны и вещества.

Переменное поле волны действует на носители заряда в ве­ществе (прежде всего на свободные электроны проводимости в металлических проводниках, электронные оболочки атомов, разноименные ионы, а также диполи в диэлектриках). При этом оказывается, что действие электрического поля в сотни раз силь­нее, чем действие магнитного поля. Это позволяет в дальнейшем не принимать во внимание магнитные свойства вещества, для объяснения которых необходимо привлекать понятия квантовой механики, и рассматривать только электрические взаимодействия, т.е., по сути, считать электромагнитную волну световым векто­ром. Поскольку электрическое поле световой волны периодичес­кое, то микроскопические заряды вещества под действием волны совершают колебания. Энергия этих колебаний частично переда­стся другим частицам среды, в результате происходит поглощение излучения; вещество нагревается. С другой стороны колеблющие­ся заряды, как и всякие ускоренные, излучают свои вторичные волны. Так осуществляется распространение электромагнитной волны.

При этом следует иметь в виду, что упомянутые выше не гели зарядов вещества находятся под действием внутреннего поля ядер атомов. Типичное значение напряженности такого поля в зонах расположения наиболее слабо связанных в атомах внешних электронов, например, для неполярных диэлектриков составляет Е_а ≈ 10¹¹ В/м. Оказывается, что взаимодействие электромагнитного излучения с веществом качественно различа­ется для волн с различными значениями напряженности E₀. Если Е₀ << Е_а, то возбужденный электрон вещества совершает гармонические колебания около своего положения равновесия. При этом возникает переменный электрический дипольный момент 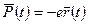, где е - заряд электрона, 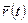- отклонение электрона от положения равновесия. Среднее значение суммы всех электронных дипольных моментов, отнесенное к объему диэлектрика определяет его поляризованность 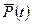, При этом между 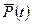- характеристикой вещества и 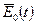- характерис­тикой излучения - существует линейная связь:

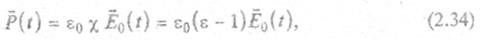где χ - диэлектрическая восприимчивость; ε - диэлектрическая . проницаемость вещества, ε = 1 – χ.

Процессы взаимодействия электромагнитных волн (света) с веществом, для которых справедливо условие Е₀ << Е_а или (2.34) относятся к линейной оптике.

Область линейной оптики включает в себя все нелазерное излучение (свет), для которого E₀ ≤ 10...10^-3 В/м, и радиоволны всех диапазонов. Если же при излучении могут достигаться напряженности поля Е₀ ≥ 10⁹...10¹⁰ В/м, (что обеспечивают многие лазеры), то соответствующие процессы рассматриваются в нелинейной оптике.

Главные особенности линейной оптики состоят в том, что ха­рактер происходящих процессов не зависит от интенсивности света, а при прохождении волны через среду частота волны не изменяется. При этом другие характеристики волны (длина вол­ны, скорость распространения) изменяются. Может изменяться также поляризация волны. В линейной оптике исходя из электри­ческих свойств вещества и свойств электромагнитной волны объясняются такие свойства света как дисперсия, рассеяние, пог­лощение и др., а также выводятся хорошо известные законы отра­жения и преломления.

Рассмотрим вывод законов отра­жения и преломления света, получа­емых в школьном курсе физики из геометрических представлений. Напомним, что нас интересует здесь лишь световой вектор, т.е. волна вектора 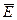. Среды, на границе которых происходит отражение и преломление волны, характеризуются различной диэлектрической проницаемостью е; соответственно ε₁ и ε2 (рис. 2.20).

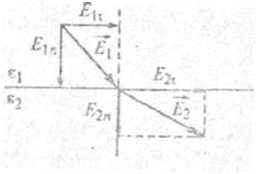Рис. 2.20.

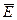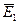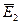Граничное условие для светового вектора состоит в том, что тангенциальные составляющие векторов и равны:

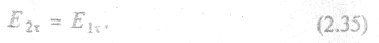
Представим световые векторы волн их волновыми векторами (рис, 2.21). Пусть падающая волна плоская монохроматическая, тогда (2.24).

Аналогично записываются выражения для векторов отраженной (индексы со штрихом) и преломленной (индексы с двумя штри­хами) волн, каждый вектор можно разложить на три ортогональ­ные компоненты по осям X, Y, Z. Од­нако, с учетом граничного условия (2.35) мы можем ограничиться лишь проекциями на ось X С учетом этого падающая волна

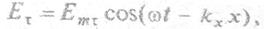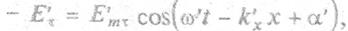отражения

преломленная

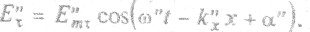
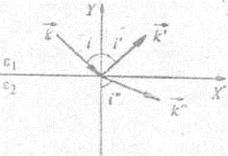Рис. 2.21.

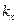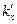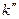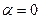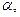
Здесь , , - проекции соответствующих волновых векторов на ось X; , 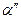- начальные фазы волн; 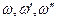- их частоты.

Поле в «верхней» среде определяется падающей и отраженной волнами. 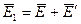- поле в «нижней» среде - только преломленной волной 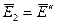. Тогда по граничному условию (2.35)

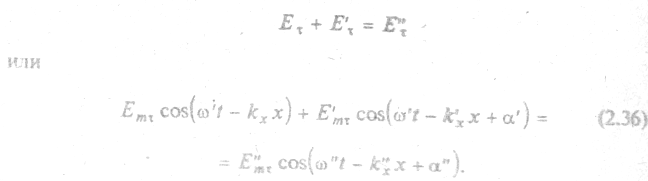
Это условие должно выполняться всегда, т.е. при любом зна­чении t. Для этого необходимо, чтобы 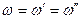, т.е. частота волны при отражении и преломлении не изменяется. Условие (3.36) должно выполняться также при любом значении х. Для этого необходимо, чтобы 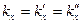; непосредственно из рис. 2.21 следует, что

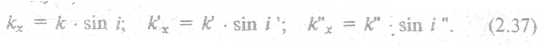
Волны (падающая и отраженная) распространяются в одной и той же среде, поэтому волновые числа их равны: 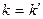. Тогда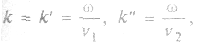

где 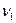- скорость распространения света в «верхней» среде, 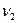- в «нижней». Таким образом, по (2.37)

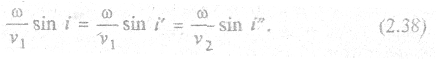Отсюда непосредственно следуют законы геометрической оптики: 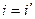, т.е. угол падения равен углу отражения;

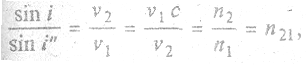т.е. отношение синуса угла падения к синусу угла преломления равно отношению абсолютных показателей преломления* (* Абсолютный показатель преломления среды равен отношению скорости света в вакууме к скорости света в данной среде) «нижней» и «верхней» сред, или относительному показателю преломления.

Выясним смысл показателя n₂₁. Скорость распространения электромагнитной волны в среде

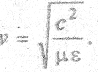
Предположим, что среды не проявляют магнитных свойств, т.е. их магнитные проницаемости 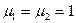. Тогда

что еще раз показывает тесную связь электрических и оптических явлений.