Наименьший радиус гиба и устойчивость труб
В практике возникает необходимость гнуть трубы с наименьшим возможным радиусом гиба. Наименьший радиус гиба зависит от механических свойств материала трубы, отношения толщины стенки трубы к величине диаметра, способа гнутья. Наиболее важным физико-механическим фактором, определяющим наименьший возможный радиус гиба, является пластические свойства металла. Пластические свойства металла трубы, подлежащей гнутью, оцениваются величиной остаточного относительного удлинения на расчетной длине при растяжении. Поэтому в каждом отдельном случае рекомендуется проверить и установить величину относительного удлинения волокон на растянутой внешней части гиба. Проверка может быть произведена путем испытания образцов труб или при помощи расчета.
Испытание труб на растяжение производится по ГОСТ 1497-61 на продольном образце (в виде полосы, вырезанной из трубы) - нормальном или пропорциональном, длинном или коротком, по усмотрению завода-изготовителя, в невыправленном виде.
При расчете мы исходим из того, что во время изгиба трубы волокна ВВ (фиг. 2) внутренней части гиба укорачиваются, а волокна АА внешней части гиба удлиняются. Величина остаточной деформации в первом приближении, если не учитывать данные, полученные Б. С. Дмитриевым, а также реализацию трубы и считать, что начало и конец деформации совпадают с началом и концом изгиба, может быть подсчитана из простого геометрического соотношения размеров.
Длина нейтрального слояL=αR=const
Длина волокон наружной части гиба после гибки L1=α(R-r)
Длина волокон внутренней части гиба после гибки L2=α(R-r)
Средняя величина относительного удлинения или сжатия
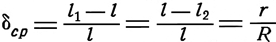
При выборе наименьшего радиуса гиба следует учесть то наибольшее относительное удлинение, которое допускает материал трубы, и сравнить его с найденной расчетной величиной.
В табл. 2 приведены значения величин относительного удлинение у стальных бесшовных горячекатаных труб.
Таблица, 2
Величина относительного удлинения материала стальных бесшовных
горячекатаных труб
| Марка стали | Относительное удлинение образца длинного пропорционального в % | Относительное удлинение образца короткого пропорционального в % |
| 10; Ст. 2 20; 20Г; Ст.4 35; Ст.5 45; Ст.6; 12ХН2А 30ХМА С Д | - |
Приведенные относительные удлинения могут служить при изгибе трубы только для сравнения: чем больше удлинение стали при разрыве, тем меньше может быть допущен радиус гиба. Однако непосредственный выбор наименьшего радиуса гиба путем использования данных об удлинении образцов при разрыве может привести к завышению наименьшего радиуса гиба, т. к. деформации удлинения волокон при изгибе происходят в более благоприятных условиях, чем при растяжении.
Под действием возникающих при изгибе сжимающих сил на внутренней части гиба образуются гофры, а в ряде случаев — складки. Появляется потеря устойчивости трубы. При таких изменениях формы трубы увеличивается сопротивление движению прорения и коррозии трубопроводов. Кроме того, наличие потери устойчивости трубы приводит к ее ослаблению как несущей конструкции.
Поведение трубы при изгибе зависит от геометрического безразмерного па-раметра (коэффициента)
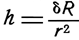
Чем меньше коэффициент h в гибе, тем более высокие требования предъявляются к средствам поддерживания формы поперечного сечения трубы и устойчивости ее стенки.
Появление потери устойчивости больше всего наблюдается у тонкостенных труб большого диаметра.
Процесс потери устойчивости может быть уяснен, если предположить, что труба до гнутья представляет собой круговой цилиндр с радиусами кривизны цилиндра р2=r и образующей р1=∞ ; тогда можно записать, что Гауссова кривизна
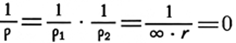
При гибке трубы вокруг гибочного ролика в месте контакта трубы с роликом образуется вмятина под действием сосредоточенной нагрузки. При образовании вмятины образующая цилиндра искривляется. При отсутствии деформации удлинения и сжатия Гауссова кривизна остается без изменений, равной нулю. Поэтому появление кривизны образующей сопровождается потерей кривизны направляющей (окружности), пересекающей ее.
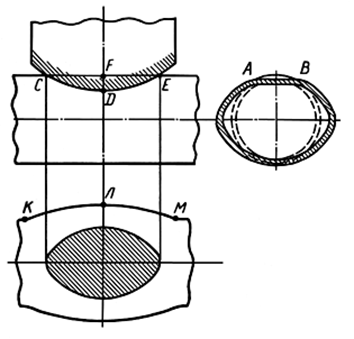
Фиг. 6. Схема потери устойчивости при гнутье трубы.
Так как прямая АВ (фиг. 6) короче дуги АВ, то волокна в ней сжаты, а кривая СDЕ длиннее образующей СFЕ, то волокна в ней растянуты. Сжатие волокон АВ является одной из причин потери прямолинейности поперечной прямой, проходящей через точку D. Образующая КЛМ в горизонтальной плоскости также искривляется и картина в ней развивается так же. Шаг гофра при данном диаметре находится в прямой зависимости от толщины стенки.
арактер изменения цилиндрической формы трубы под действием сосредоточенной нагрузки виден из следующих опытов автора. Трубы диаметром 95 мм с толщиной стенки 1 мм и диаметром 38 мм с толщиной стенки 1,55 мм нагружались сосредоточенной силой. Измерения перемещений велись по двум взаимно-перпендикулярным направлениям. Установлено, что под действием сосредоточенной силы образуются волны различной длины и амплитуды, происходит деформация всей оболочки; при этом в двух взаимно-перпендикулярных сечениях вдоль оси трубы, волны имеют противоположные по знаку амплитуды (фиг. 7).
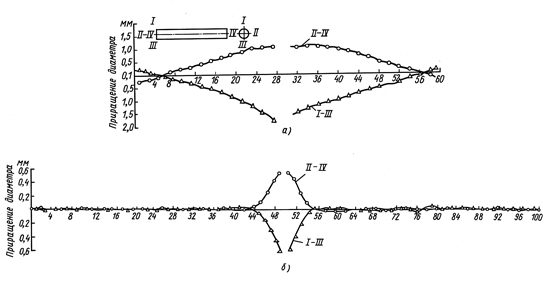
Фиг.7. Перемещение двух взаимно-перпендикулярных образующих при сжатии:
а — трубы диаметром 98 мм с толщиной стенки 1 мм; б — трубы диаметром 38 мм с толщиной стенки 1,55 мм.
Ввиду того, что амплитуды различны по знаку, в ряде кольцевых сечений амплитуды обеих волн приближаются к нулю и размеры оболочки по диаметрам в этих кольцевых сечениях остаются неизменными.
Волны имеют наибольшую амплитуду в обоих сечениях, где приложена нагрузка, затем она затухает. Сравнивая волны двух труб с различным отношением
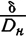 видим (фиг. 7, а и б), что чем меньше это отношение, тем медленней затухает волна.
видим (фиг. 7, а и б), что чем меньше это отношение, тем медленней затухает волна.
При действии различных по величине и одинаковых по месту приложения нагрузок на трубу одного и того же размера характер деформаций в упругой стадии остается неизменным, отличаясь лишь по величине.
Имея очертания образующих (в двух взаимно-перпендикулярных сечениях вдоль оси трубы), полученных путем измерения перемещений при действии одной и той же по величине сосредоточенной силы, приложенной как на конце трубы, так и в середине, и совместив эти кривые, легко найти окрестности кольцевого сечения, в котором пересекаются данные кривые. Эти окрестности являются теми местами, где должны быть расположены опоры при изгибе трубы, что позволит получить наиболее равномерные деформации по всей длине трубы. Этот вывод проверялся путем приложения двух равных по величине сосредоточенных нагрузок на трубу. Выявлено, что наиболее равномерные деформации наблюдаются тогда, когда от концов трубы нагрузки приложены на определенном расстоянии. Из этих исследований становится очевидным, что при разработке оснастки для гибки тонкостенных труб размер гибочного ролика, прижимных планок и расстановка опор должна производиться с учетом образования волн на трубе. Так, например, при гибке труб диаметром 98, с толщиной стенки 1 мм на двух опорах уменьшение деформаций происходит тогда, когда опоры расположены на расстоянии 1/3 длины трубы от ее концов.
Кроме того, следует учесть, что сохранение первоначальной кривизны поперечного сечения трубы в опасной сжимаемой зоне (внутренняя часть гиба) представляется важным условием борьбы с образованием гофр во время гибки. При существующих формах внешних поддерживающих устройств, когда они выполняются по полуокружности, прилегающей к трубе, длина поддерживающего участка должна быть не менее длины волны с наибольшими перемещениями.
До настоящего времени не решен вопрос о количественной оценке допустимых размеров гофр, влияющих на уменьшение прочности изогнутой трубы. Поэтому размеры гофр выбираются на основе опытных данных.
В судостроении для труб диаметром до 120 мм введен допуск на образование гофр. В зависимости от внутреннего давления транспортируемого продукта гофры не должны .превышать следующий процент от наружного диаметра трубы: до 2 кг/см2 — 6%, от 2 до 16 кг/ см2 — 3 и более, 16 кг/ см2 — не более 2%.
Приведено решение задач о потере устойчивости труб при гибке. Однако этими данными трудно пользоваться Ввиду наличия разностенности, первоначальной овальности, разброса прочностных характеристик в одной и той же партии труб, а также из-за контактных напряжений между рабочим инструментом станка и трубой.
Для расчета могут быть приняты только приближенные формулы. Так, например, Я.3. Скоморовским установлена зависимость критической нагрузки от прочностных и геометрических параметров стальных труб с относительной толщиной стенки
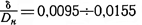 при разных схемах нагружения.
при разных схемах нагружения.
Если труба в радиальном направлении не имеет ограничителя и изгиб производится двумя парами сил (чистый изгиб), то величина критического изгибающего момента Мкр, при котором наступит местная потеря устойчивости стенки труб, определяется формулой

При изгибе трубы как консоли силой Р на конце (поперечный изгиб), когда сечение трубы в заделке защемлено по всему контуру, величина критического момента Мкр = PL (L— длина консоли ) выражается формулой

Если труба подвержена одновременному нагружению осевой силой и изгибающим моментом, то при известной осевой силе Р, величина максимально допускаемого изгибающего момента М будет
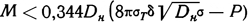
В этом же случае при известном изгибающем моменте величина допускаемой осевой силы будет
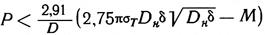
При изгибе трубы вследствие эксцентричного сжатия силой Р величина безопасного эксцентрицитета е, определяется формулой
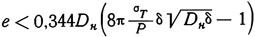
Дата добавления: 2017-11-21; просмотров: 2562;











