Производная по направлению.

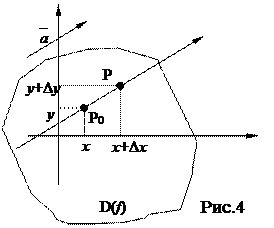
Рассмотрим дифференцируемую функцию z = f(x, y) и произвольный вектор 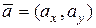. Пусть точка Р₀(х, у) Î D(f). Через точку Р₀ в направлении вектора 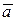проведем ось и на этой оси возьмем произвольную точку 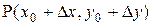Î D(f) (рис.4).

Обозначим

| P₀P| = .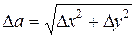

При переходе от точки Р₀ к точке Р функция z = f(x, y) получит приращение

Dz = f(x+Dх, у + Dy) – f(x, y)

Определение 8.1. Предел вида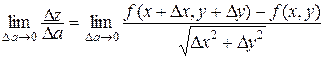

(если он существует) называется производной от функции 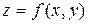в точке Р по направлению вектора 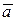(направленной производной) и обозначается .

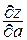Итак, по определению

= .

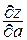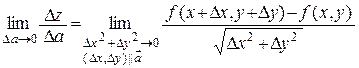Так как 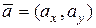, то направляющие косинусы этого вектора равны

, .

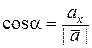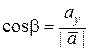Используя определение дифференцируемости функции, можно доказать, что

.

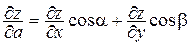Исходя из равенства 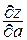= 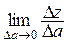и физического смысла предела 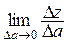(пределы такого вида мы рассматривали при изучении производной функции одной переменной), приходим к выводу, что с физической точки зрения, производная по направлению характеризует скорость изменения функции в направлении заданного вектора.

Тогда, если` 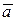=`i , то cosa = 1, cosb = 0, значит ;

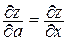если 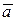=`j, то cosa = 0, cosb = 1 и .

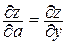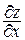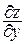Следовательно, частные производные и функции z = f(x, y) по ее аргументам характеризуют скорость изменения функции в направлении соответственно осей ОХ и ОУ. Это определяет физический смысл частных производных функции двух переменных.

Аналогично можно дать определение производной по направлению функции трех переменных.

Определение 8.2. Предел вида

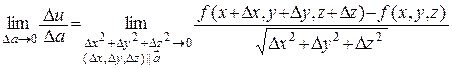
(если он существует) называется производной от функции и = f(x, y, z) по направлению вектора ` 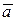и обозначается .

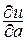Эта производная вычисляется по формуле

,

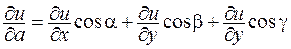где 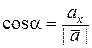, , 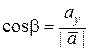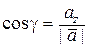направляющие косинусы вектора 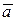= (а_х , а_у , а_z).

Пример 1:

Задана функция 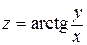и точка 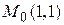. Требуется найти производную по направлению вектора 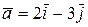в точке .

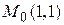Решение. Найдем частные производные данной функции:

.

.

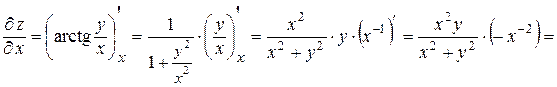
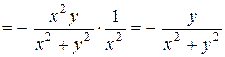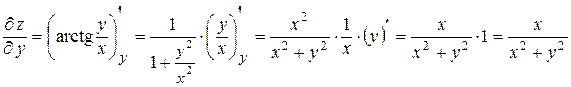Вычислим значения этих производных в точке :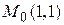

= ,

= .

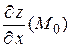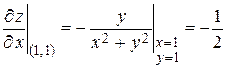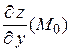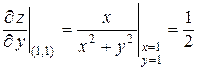Производную функции z в точке 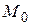по направлению вектора 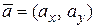найдем по формуле

,

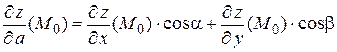где .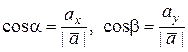

Вычислим направляющие косинусы заданного вектора :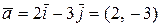

,

.

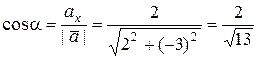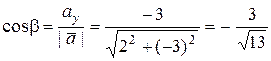Значения частных производных функции в точке 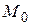нам уже известны:

= , = .

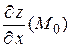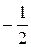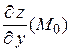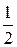Тогда искомая производная по направлению в точке 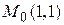равна

.

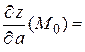
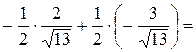
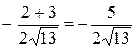С физической точки зрения этот результат означает следующее: функция при переходе через точку 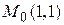в направлении вектора 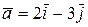убывает (производная отрицательная).