Производная и монотонность функции
Приложения производной к исследованию функций
Применение производной для нахождения промежутков монотонности, точек экстремума, наибольшего и наименьшего значений позволяют учащимся понять ценность производной как средства исследования функции.
Производная и монотонность функции
Рассмотрим графики функций. Что можно сказать о производных этих функций в области их определения? (На доске провести касательные)

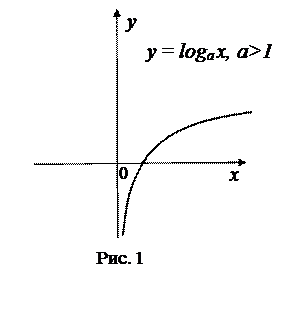
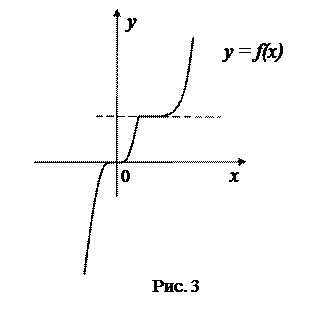
Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство 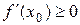 (причём равенство
(причём равенство 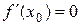 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция
выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция 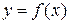 возрастает на промежутке Х.
возрастает на промежутке Х.
Аналогично формулируется теорема 2. Если во всех точках открытого промежутка Х выполняется неравенство 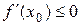 (причём равенство
(причём равенство 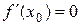 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция
выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция 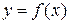 убывает на промежутке Х.
убывает на промежутке Х.
Сразу обратим внимание на то, что теорема сформулирована для функций, непрерывных на промежутке Х (что следует из их дифференцируемости ).
В учебниках А.Г. Мордковича доказательство этих теорем не приводится. В учебнике А.Н. Колмогорова авторы не отказываются от доказательства. Оно основано на формуле Лагранжа, смысл которой разъясняется, исходя из графических представлений.
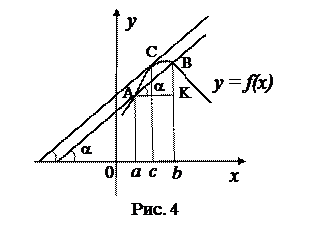
Пусть А и В – точки графика непрерывной функции с абсциссами а и b соответственно. Определим угловой коэффициент прямой АВ.
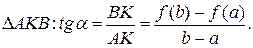
Проведём касательную, параллельную АВ. с – абсцисса точки касания.
Угловой коэффициент касательной равен 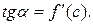 Таким образом,
Таким образом,
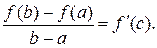
Теперь обратимся к доказательству теоремы.
Дано: функция у = f(x), 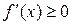 при хÎХ. (В учебнике Колмогорова неравенство строгое)
при хÎХ. (В учебнике Колмогорова неравенство строгое)
Доказать: функция возрастает на Х.
Доказательство
Рассмотрим два значения х1 и х2, принадлежащие промежутку Х, причём
х1 < х1. сравним f(x1) и f(x2). По формуле Лагранжа 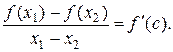
х1 - х2<0, 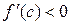 , так как с Î Х, следовательно, f(x1) - f(x2)< 0, f(x1) < f(x2), то есть меньшему значению аргумента соответствует меньшее значение функции: по определению функция f возрастает на Х.
, так как с Î Х, следовательно, f(x1) - f(x2)< 0, f(x1) < f(x2), то есть меньшему значению аргумента соответствует меньшее значение функции: по определению функция f возрастает на Х.
Аналогично доказывается теорема об убывании функции.
 Наконец, задумаемся о монотонности функции на закрытом промежутке. Пусть Х = [a,b]. Обратимся к рисункам 5, 6.
Наконец, задумаемся о монотонности функции на закрытом промежутке. Пусть Х = [a,b]. Обратимся к рисункам 5, 6.
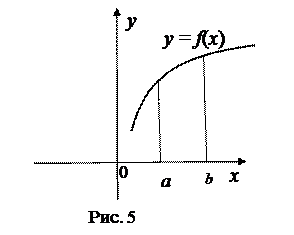
Можно ли утверждать, что функция у = f(x) возрастает на [a,b] на рис. 5, на рис 6? Какому условию должна удовлетворять данная функция, чтобы можно было заменить открытый промежуток на закрытый?
Ответ: она должна быть непрерывной на концах этого промежутка.
Рассмотрим функцию 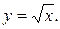
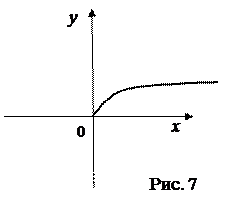
Можно ли утверждать, что она возрастает на промежутке [0; +¥)?
Ответ: нет, так как данная функция не является непрерывной (в школьном понимании) в точке 0.
И ещё одна тонкость, связанная с монотонностью функции. Можно ли утверждать, что функция 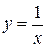 убывает при
убывает при 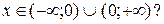
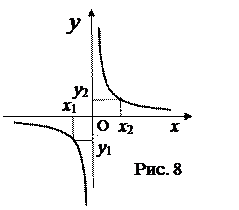
Очевидно, что данная функция убывает. Объединение промежутков даёт право взять значения х1 и х2 в каждом из них. Тогда х1 < х2 и у1 < у2: функция возрастает. Правильно: данная функция убывает на каждом из промежутков 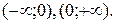
Дата добавления: 2016-06-15; просмотров: 3142;











