Производная алгебраической суммы функций.
Теорема 1.
Производная алгебраической суммы двух дифференцируемых функций равна алгебраической сумме производных этих функций.
(u(x)+v(x))' = u'(x)+v'(x).
(u(x)-v(x)'=u'(x)-v'(x).
Замечание. Можно доказать справедливость теоремы 1 для суммы любого конечного числа дифференцируемых функций, т.е.
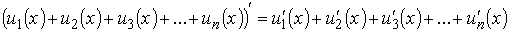
Задача: Найти производную функции f(x)=x2+x-7.
Вычислить f  (-1), f
(-1), f  (0), f
(0), f  (3)
(3)
Решение
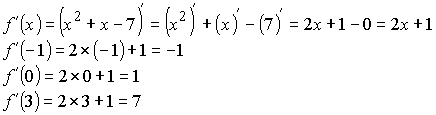
Производная произведения функций
Теорема 2.
Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой.
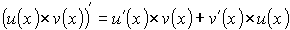 .
.
Эта формула называется формулой Лейбница.
Следствие 1. Постоянный множитель можно выносить за знак производной. 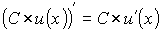 .
.
Следствие 2. Производная функции f(x)=xn, где 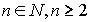 равна произведению показателя n на степень
равна произведению показателя n на степень 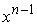 .
.
Задача. Найти производную функции f(x)=x3(x-1)
Решение:
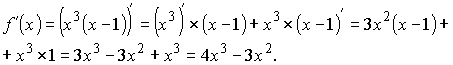
Производная частного двух функций
Теорема 3. Производную частного двух дифференцируемых функций можно найти по формуле:
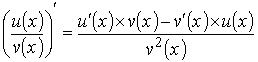 , где
, где 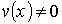
Задача: Найти производную функции
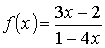
Решение:
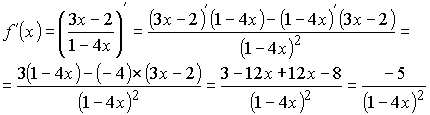
Упражнения
Найти производные функции:
1. 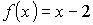
2. 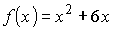
3. 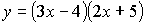
4. 
5. 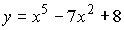
Дата добавления: 2016-06-05; просмотров: 9717;











