Пересечение поверхности плоскостью общего положения

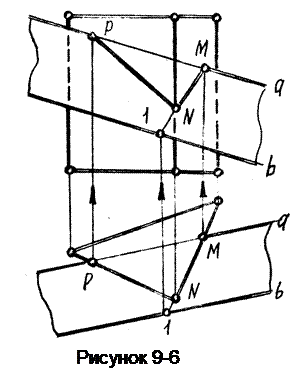Пример 7. Построить линию пересечения вертикальной призмы плоскостью общего положения Б (а//b), (рисунок 9-6).

Вся боковая поверхность призмы на виде сверху вырождается в треугольник; поэтому и сечение здесь совпадает с гранями призмы и находится в пределах отсека плоскости ограниченной линией PNМ.

Для построения этой линии на виде спереди необходимо определить положение точек M,N,P.

Точки Р и М принадлежат прямой а.Для построения т.N в плоскости Б проведем вспомогательную прямую 1-М.

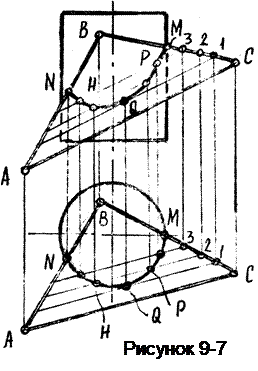Пример 8. Построить линию пересечения вертикального цилиндра плоскостью общего положения Б(АВС), (рисунок 9-7).

В данном случае имеем ответ на виде сверху, т.к. поверхность цилиндра вырождается здесь в окружность и линия пересечения совпадает с боковой поверхностью цилиндра NНQРМ.

Для построения ее на виде спереди используем ряд вспомогательных прямых в секущей плоскости, т.е. решаем задачу на построение точки на плоскости по ее заданному виду.

Видимость определяем с помощью пространственного представления.

Пример 9.Построить линию пересечения плоскости общего положения Б (а//b) с поверхностью пирамиды (рисунок 9-8). Для построения сечения найдем точки пересечения ребер пирамиды с данной плоскостью, для чего трижды решим задачу на пересечение прямой общего положения с плоскостью общего положения.

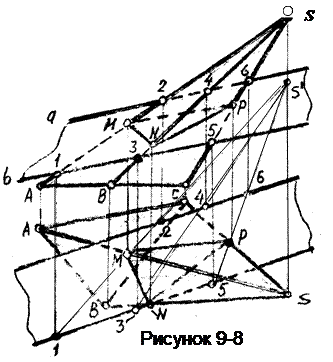Возьмем на плоскости вспомогательные прямые 1-2, 3-4 и 5-6 фронтально конкурирующие соответственно с ребрами SA, SB и SC и выясним их взаимное положение.

Так как ребра пирамиды пересекаются в одной точке S, то и все конкурирующие прямые будут пересекаться в точке S' фронтально-конкурирующей с вершиной S . В пересечении вспомогательных прямых с соответствующими ребрами пирамиды находим вершины сечения, которые соединяем с учетом видимости отрезками прямых.

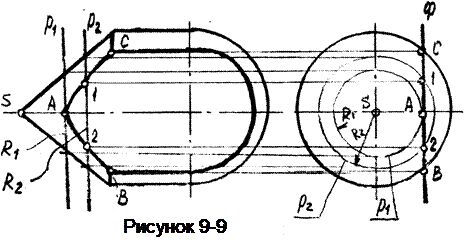Пример 10. Рассмотрим построение линии среза технической детали, ограниченной несколькими поверхностями, одной фронтальной плоскостью Ф (рисунок 9-9).

Деталь представляет собой некоторое тело вращения, ограниченное поверхностью конуса, цилиндра и шара. Точки линии среза на поверхности конуса строятся при помощи параллелей р. Построение начинаем с нахождения крайней левой точки, для чего проводим на виде слева параллель р1, касательную к плоскости среза (радиуса R1) и находим ее положение на виде спереди. Для построения остальных точек проводим ряд параллелей, начиная их построение с вида спереди. Затем строим их на виде слева и находим точки пересечения с фронтальной плоскостью - это и будут точки линии среза.

Линия среза на цилиндре представляет собой пару прямых, а- на сфере - окружность, для построения которых точки находить не нужно.