Интегрирование линейных неоднородных дифференциальных уравнений
Интегрирование линейных однородных дифференциальных уравнений.
Пусть в линейном однородном дифференциальном уравнении
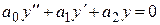
коэффициенты 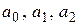 – постоянные числа. Для таких уравнений доказано, что частные решения
– постоянные числа. Для таких уравнений доказано, что частные решения 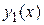 ,
, 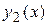 , составляющие фундаментальную систему решений, следует искать в виде
, составляющие фундаментальную систему решений, следует искать в виде 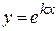 , где
, где 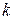 – корень характеристического уравнения.
– корень характеристического уравнения.
Определение 1
Характеристическим уравнением линейного однородного дифференциального уравнения 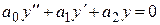 называется алгебраическое уравнение второй степени
называется алгебраическое уравнение второй степени
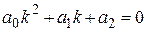 . (1)
. (1)
Характеристическое уравнение линейного дифференциального уравнения второго порядка есть квадратное уравнение, для составления которого достаточно в дифференциальном уравнении 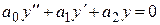 заменить
заменить 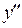 на
на 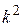 ,
, 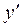 – на
– на 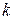 , а
, а 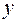 заменить на 1.
заменить на 1.
Как известно, при решении квадратного уравнения возможны три случая:
· корни 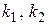 этого уравнения действительные и различные:
этого уравнения действительные и различные: 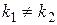 ;
;
· корни 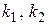 действительные и равные:
действительные и равные: 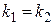 ;
;
· корни 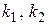 есть комплексно-сопряженные числа:
есть комплексно-сопряженные числа: 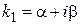 ,
, 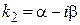 .
.
Структура фундаментальной системы решений { 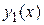 ,
, 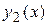 }, а вместе с ней и общего решения дифференциального уравнения (1), зависит от вида корней характеристического уравнения. Эта зависимость отражена ниже в таблице 1.
}, а вместе с ней и общего решения дифференциального уравнения (1), зависит от вида корней характеристического уравнения. Эта зависимость отражена ниже в таблице 1.
Таблица 1
| Корни характеристического уравнения | Фундаментальная система решений | Вид общего решения |
I. Действительные различные 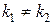
| 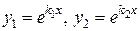
| 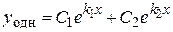
|
II. Действительные равные 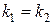
| 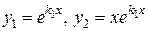
| 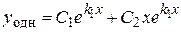
|
III. Комплексно- сопряженные
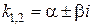
| 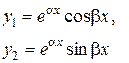
| 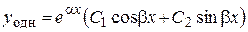
|
Предлагаем следующий порядок решения линейного однородного дифференциального уравнения:
1) Составить характеристическое уравнение для заданного дифференциального уравнения и найти его корни.
2) Записать функции 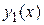 ,
, 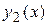 , составляющие фундаментальную систему решений.
, составляющие фундаментальную систему решений.
3) Записать общее решение 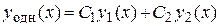 .
.
Для записи функций ФСР и общего решения используйте таблицу 3.
Пример 1.Решить дифференциальное уравнение 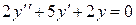 .
.
Решение
Будем придерживаться сформулированного алгоритма.
1) Составим характеристическое уравнение для данного линейного дифференциального уравнения. Для этого в уравнении 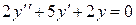 заменим
заменим 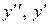 и
и 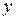 соответственно на
соответственно на 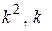 и 1, получим
и 1, получим
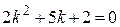 .
.
Найдем корни этого уравнения*):
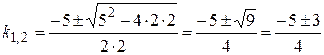 ,
,
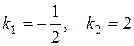 .
.
2) Полученные корни 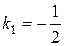 ,
, 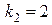 действительные и различные, следовательно, имеем случай I таблицы 1, поэтому фундаментальную систему решений образуют функции
действительные и различные, следовательно, имеем случай I таблицы 1, поэтому фундаментальную систему решений образуют функции
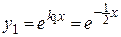 ,
, 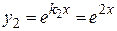 .
.
3) Тогда общим решением заданного дифференциального уравнения является функция
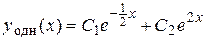 .
.
Ответ: 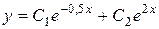
Пример 2Найти решение уравнения 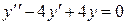 , удовлетворяющее условиям
, удовлетворяющее условиям 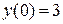 ,
, 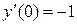 .
.
Решение
Согласно правилу решения задачи Коши вначале найдем общее решение данного уравнения.
1) Составим и решим характеристическое уравнение:
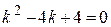 ,
, 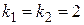 .
.
2) Корни характеристического уравнения действительные и равные (случай IIтаблицы 1), следовательно, фундаментальную систему решений образуют функции
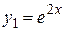 ,
, 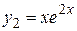 .
.
3) Тогда общее решение заданного дифференциального уравнения имеет вид
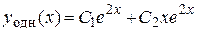 .
.
Теперь найдем искомое частное решение. Для этого нужно найти значения постоянных 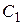 и
и 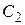 Чтобы определить эти значения, найдем производную функции
Чтобы определить эти значения, найдем производную функции 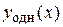 :
:
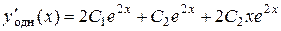 ,
,
и подставим заданные начальные условия 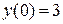 ,
, 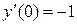 в равенства
в равенства
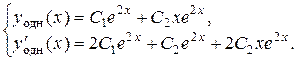
Получим систему уравнений относительно неизвестных 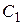 и
и 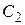 :
:
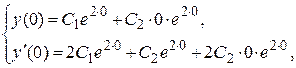 Þ
Þ 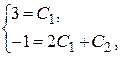
Решив эту систему, найдем значения 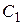 и
и 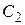 :
:
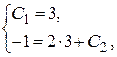 Þ
Þ 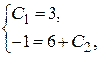 Þ
Þ 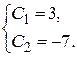
Подставим найденные значения 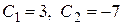 в общее решение
в общее решение 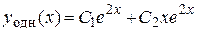 , получим искомое частное решение:
, получим искомое частное решение:
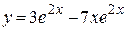 .
.
Ответ: 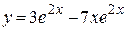
Пример 3 Решить дифференциальное уравнение 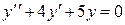 .
.
Решение
Характеристическое уравнение для данного дифференциального уравнения имеет вид
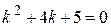 .
.
Решим это уравнение:
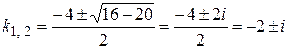 .
.
Получили комплексно-сопряженные корни (случай III таблицы 1), где 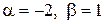 . Значит, фундаментальная система решений состоит из функций
. Значит, фундаментальная система решений состоит из функций
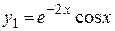 ,
, 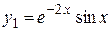 .
.
Тогда общее решение данного дифференциального уравнения имеет вид
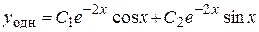 .
.
Ответ: 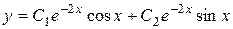 .
.
Замечание. Для линейных однородных дифференциальных уравнений
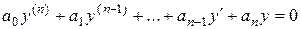
порядка выше двух ( 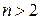 ) общее решение, аналогично уравнению второго порядка, представляет собой линейную комбинацию фундаментальной системы решений этого уравнения:
) общее решение, аналогично уравнению второго порядка, представляет собой линейную комбинацию фундаментальной системы решений этого уравнения:
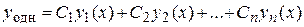 .
.
Функции 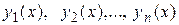 *) фундаментальной системы решений также можно найти с помощью корней характеристического уравнения, которое для уравнения п-го порядка имеет вид
*) фундаментальной системы решений также можно найти с помощью корней характеристического уравнения, которое для уравнения п-го порядка имеет вид
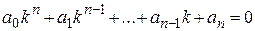 .
.
Пример 4 Решить дифференциальное уравнение
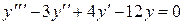 .
.
Решение
Запишем характеристическое уравнение:
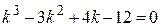 .
.
Чтобы найти корни этого уравнения, разложим на множители его левую часть, используя способ группировки и вынесения общего множителя:
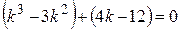 ,
, 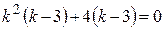 ,
,
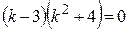 .
.
Приравнивая к нулю каждый из множителей, получаем:
1) 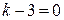 Þ
Þ 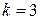 ;
;
2) 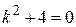 – это уравнение действительных корней не имеет, поскольку
– это уравнение действительных корней не имеет, поскольку 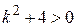 .
.
Но так как всякое алгебраическое уравнение имеет столько корней, какова его степень (в общем случае комплексных), то уравнение 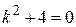 имеет два комплексных корня. Найдем их
имеет два комплексных корня. Найдем их
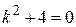 Þ
Þ 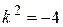 Þ
Þ 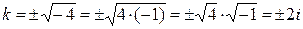 .
.
Итак, характеристическое уравнение имеет три корня:
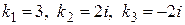 .
.
Запишем фундаментальную систему решений заданного дифференциального уравнения. Действительному корню 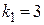 в фундаментальной системе соответствует функция–решение
в фундаментальной системе соответствует функция–решение 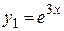 . Паре комплексно-сопряженных корней
. Паре комплексно-сопряженных корней 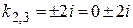 соответствуют два действительных решения
соответствуют два действительных решения
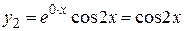 ,
, 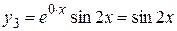 .
.
Следовательно, общее решение заданного дифференциального уравнения имеет вид
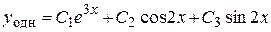 .
.
Ответ: 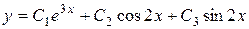 .
.
Пример 5 Решить дифференциальное уравнение 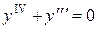 .
.
Решение
Характеристическое уравнение 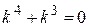 , или
, или 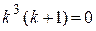 имеет корни
имеет корни 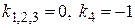 . Тогда фундаментальную систему решений образуют функции-решения
. Тогда фундаментальную систему решений образуют функции-решения
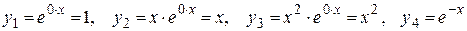 .
.
Значит, общее решение данного дифференциального уравнения имеет вид
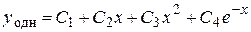 .
.
Ответ: 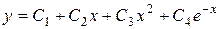
Интегрирование линейных неоднородных дифференциальных уравнений
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка
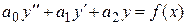 (3.6),
(3.6),
где 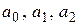 – действительные числа,
– действительные числа, 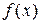 непрерывная на некотором интервале
непрерывная на некотором интервале 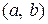 функция.
функция.
Согласно теореме 3.3 о структуре общего решения линейного неоднородного дифференциального уравнения, общее решение уравнения (3.6) можно найти в виде 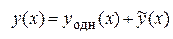 , где
, где 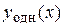 –общее решение соответствующего однородного уравнения, а
–общее решение соответствующего однородного уравнения, а 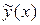 – какое-либо частное решение уравнения (3.6).
– какое-либо частное решение уравнения (3.6).
Отыскание общего решения 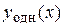 линейного однородного дифференциального уравнения рассмотрено в предыдущем пункте. Следовательно, остается решить вопрос нахождения какого-либо частного решения
линейного однородного дифференциального уравнения рассмотрено в предыдущем пункте. Следовательно, остается решить вопрос нахождения какого-либо частного решения 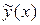 линейного неоднородного дифференциального уравнения.
линейного неоднородного дифференциального уравнения.
Для линейных неоднородных уравнений с постоянными коэффициентами в случае, когда правая часть – функция 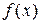 – имеет так называемый «специальный вид» (таблица 4), можно применить метод подбора частного решения. Суть метода заключается в следующем: по виду функции
– имеет так называемый «специальный вид» (таблица 4), можно применить метод подбора частного решения. Суть метода заключается в следующем: по виду функции 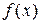 и корням характеристического уравнения подбирается вид функции
и корням характеристического уравнения подбирается вид функции 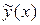 с неопределенными коэффициентами, которые затем определяются в результате подстановки
с неопределенными коэффициентами, которые затем определяются в результате подстановки 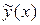 в заданное уравнение исходя из условия, что
в заданное уравнение исходя из условия, что 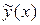 удовлетворяет уравнению (3.6) .
удовлетворяет уравнению (3.6) .
На практике для подбора функции 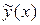 можно использовать таблицу 2.
можно использовать таблицу 2.
Рассмотрим примеры решения линейных неоднородных уравнений, придерживаясь алгоритма, сформулированного на странице 51.
Пример 6 Найти общее решение дифференциального уравнения
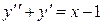 .
.
Решение. Данное уравнение есть линейное неоднородное дифференциальное уравнение второго порядка. Согласно теореме 3.3, общее решение этого уравнения будем искать в виде
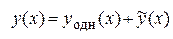 ,
,
где 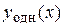 – общее решение соответствующего однородного уравнения, а
– общее решение соответствующего однородного уравнения, а 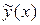 – какое-либо частное решение заданного уравнения.
– какое-либо частное решение заданного уравнения.
1) Найдём решение 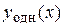 . Для этого составим и решим линейное однородное дифференциальное уравнение, соответствующее данному:
. Для этого составим и решим линейное однородное дифференциальное уравнение, соответствующее данному:
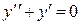 .
.
Характеристическое уравнение 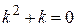 , или
, или 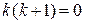 , имеет корни
, имеет корни 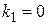 ,
, 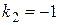 . Поэтому (согласно правилу, сформулированному на странице 53, таблица 3) общее решение имеет вид
. Поэтому (согласно правилу, сформулированному на странице 53, таблица 3) общее решение имеет вид
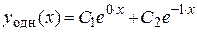 , или
, или 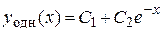 .
.
2) Найдем частное решение 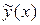 исходного дифференциального уравнения.
исходного дифференциального уравнения.
Функцию 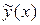 подберем по виду правой части данного дифференциального уравнения и корням соответствующего характеристического уравнения, ориентируясь на таблицу 4.
подберем по виду правой части данного дифференциального уравнения и корням соответствующего характеристического уравнения, ориентируясь на таблицу 4.
Таблица 4
Вид правой части 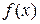
| Корни характеристического уравнения | Вид частного решения 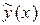
|
I. 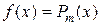 , ,
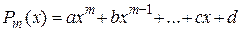 – многочлен степени т,
а, b,…,c, d – известные числа
– многочлен степени т,
а, b,…,c, d – известные числа
| а) Число 0 неявляется корнем характеристического уравнения | 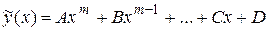 . .
|
| б) Число 0 – корень характеристического уравнения кратности r | 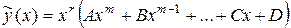
| |
II. 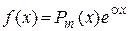 , ,
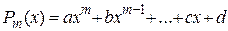 – многочлен степени т,
α, а, b,…,c, d – известные числа. – многочлен степени т,
α, а, b,…,c, d – известные числа.
| а) Число aне является корнем характеристического уравнения | 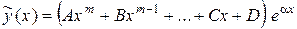 . .
|
| б) Число a – кореньхарактеристического уравнения кратности r | 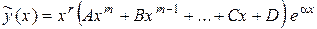 . .
| |
III. 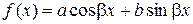 ,
а, b, β– известные числа. ,
а, b, β– известные числа.
| а) Числа 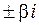 не являются корнями характеристического уравнения, не являются корнями характеристического уравнения,
| 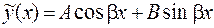 . .
|
б) Числа 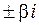 – корни характеристического уравнения кратности r – корни характеристического уравнения кратности r
| 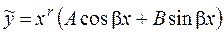 . .
| |
IV. 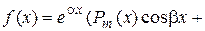
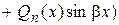 Рт(х) и Qп(x) – многочлены степени т и п соответственно
Рт(х) и Qп(x) – многочлены степени т и п соответственно
| а) Числа 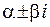 не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 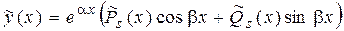 , ,
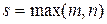 . .
|
б) Числа 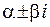 – корнихарактеристического уравнения кратности r – корнихарактеристического уравнения кратности r
| 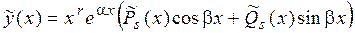 , ,
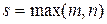 . .
| |
Здесь А, В, С, D – неизвестные буквенные коэффициенты, 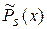 , , 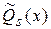 – многочлены степени s с буквенными коэффициентами. – многочлены степени s с буквенными коэффициентами.
|
Правая часть уравнения – функция 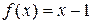 – есть функция вида
– есть функция вида 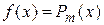 , где
, где 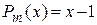 – многочлен первой степени. Так как число
– многочлен первой степени. Так как число 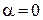 является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 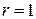 , то имеем случай I,б) таблицы 4. Значит, частное решение будем искать в виде
, то имеем случай I,б) таблицы 4. Значит, частное решение будем искать в виде
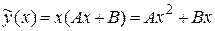 .
.
Неопределенные коэффициенты А и В найдем из условия, что функция 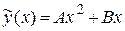 является решением заданного уравнения, а значит, при подстановке этой функции в уравнение оно обращается в верное равенство.
является решением заданного уравнения, а значит, при подстановке этой функции в уравнение оно обращается в верное равенство.
Найдем 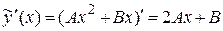 ,
, 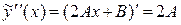 и подставим эти производные в уравнение
и подставим эти производные в уравнение 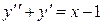 . Имеем
. Имеем
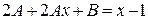 ,
, 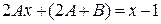 .
.
Получили равенство многочленов. Приравнивая коэффициенты при х, имеем 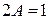 ; приравнивая свободные члены, имеем
; приравнивая свободные члены, имеем 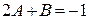 . Таким образом, получили систему уравнений относительно А и B:
. Таким образом, получили систему уравнений относительно А и B:
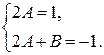
Решая эту систему, находим 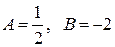 .
.
Значит, частное решение 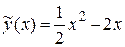 .
.
3) Запишем общее решение исходного дифференциального уравнения
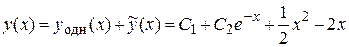 .
.
Ответ: 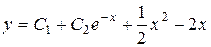 .
.
Пример 7 Решить дифференциальное уравнение 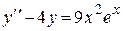 .
.
Решение
Решение данного линейного неоднородного дифференциального уравнения также ищем в виде 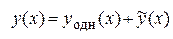 .
.
1) Найдём 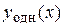 . Для этого составим и решим однородное уравнение, соответствующее данному:
. Для этого составим и решим однородное уравнение, соответствующее данному:
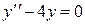 .
.
Характеристическое уравнение 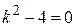 имеет корни
имеет корни 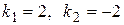 . Поэтому (согласно правилу на странице 53, таблица 3) общее решение однородного уравнения имеет вид
. Поэтому (согласно правилу на странице 53, таблица 3) общее решение однородного уравнения имеет вид
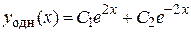 .
.
2) Найдем частное решение 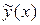 заданного уравнения. Функцию
заданного уравнения. Функцию 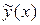 подберем по виду правой части
подберем по виду правой части 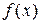 и корням характеристического уравнения.
и корням характеристического уравнения.
Правая часть дифференциального уравнения 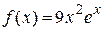 есть функция вида
есть функция вида 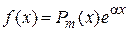 , где
, где 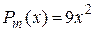 – многочлен второй степени, а
– многочлен второй степени, а 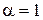 , причем a не является корнем характеристического уравнения. Значит, эта функция относится к типу II,а) таблицы 4, поэтому частное решение уравнения будем искать в виде
, причем a не является корнем характеристического уравнения. Значит, эта функция относится к типу II,а) таблицы 4, поэтому частное решение уравнения будем искать в виде
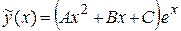 ,
,
где А, В, С – неопределенные коэффициенты.
Найдем эти коэффициенты из условия, что функция 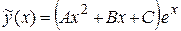 удовлетворяет заданному уравнению. Для этого найдем производные:
удовлетворяет заданному уравнению. Для этого найдем производные:
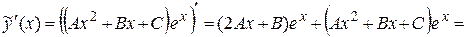
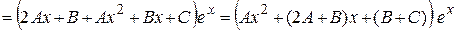 ,
,
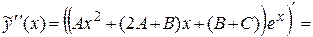
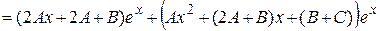 .
.
Подставим в исходное дифференциальное уравнение 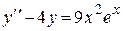 вместо у выражение
вместо у выражение 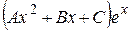 , а вместо у¢¢ – выражение
, а вместо у¢¢ – выражение 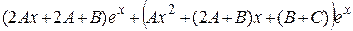 , получим
, получим
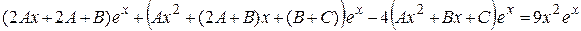 .
.
Разделим обе части этого равенства на 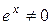 , получим
, получим
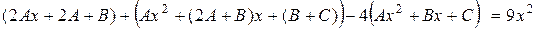 .
.
Раскроем скобки и приведем подобные в левой части равенства
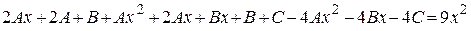 ,
,
в результате имеем
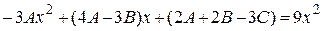 .
.
Получили равенство двух многочленов. Приравнивая коэффициенты при одинаковых степенях х многочленов в левой и правой частях равенства, получим систему относительно А, В, С:
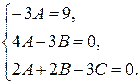
Решая эту систему, находим 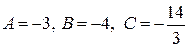 .
.
Значит, частное решение имеет вид 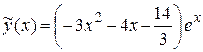 .
.
3) Тогда общее решение заданного дифференциального уравнения
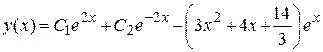 .
.
Ответ: 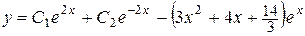
Пример 3.8 Решить дифференциальное уравнение
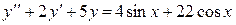 ,
, 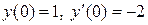 .
.
Решение
Как известно, чтобы найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, нужно, прежде всего, найти общее решение этого уравнения. Как и в предыдущих примерах, общее решение ищем в виде 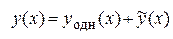 .
.
1) Составим и решим линейное однородное дифференциальное уравнение, соответствующее данному: 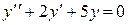 .
.
Имеем: 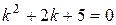 Þ
Þ 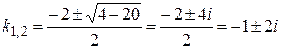 .
.
Тогда 
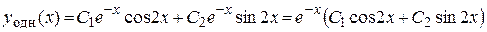 .
.
2) Найдем частное решение 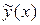 . Правая часть дифференциального уравнения
. Правая часть дифференциального уравнения 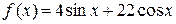 относится к виду III,a) таблицы 4:
относится к виду III,a) таблицы 4:
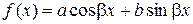 ,
,
где 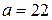 ,
, 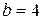 ,
, 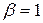 , и числа
, и числа 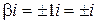 не являются корнями характеристического уравнения. Следовательно, решение
не являются корнями характеристического уравнения. Следовательно, решение 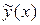 нужно искать в виде
нужно искать в виде
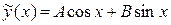
Определим коэффициенты А и В. Для этого находим
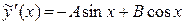 ,
,
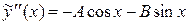 ,
,
и подставив эти соотношения в исходное дифференциальное уравнение, получим
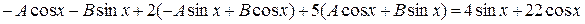 ,
,
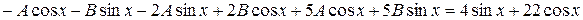 ,
,
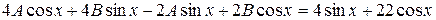 ,
,
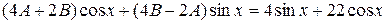 .
.
Приравнивая коэффициенты при 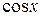 в левой и правой частях этого равенства, имеем
в левой и правой частях этого равенства, имеем 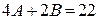 ; приравнивая коэффициенты при
; приравнивая коэффициенты при 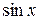 , имеем
, имеем 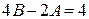 . В результате получим систему уравнений относительно А и В:
. В результате получим систему уравнений относительно А и В:
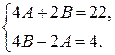
Решая эту систему, найдем 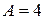 ,
, 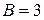 . Тогда
. Тогда
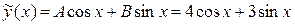 .
.
3) Следовательно, общее решение заданного дифференциального уравнения имеет вид
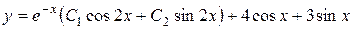 .
.
По условию, требуется найти частное решение заданного дифференциального уравнения, удовлетворяющее начальным условиям 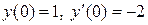 , а это значит: нужно найти такие значения постоянных
, а это значит: нужно найти такие значения постоянных 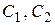 , чтобы найденная функция
, чтобы найденная функция
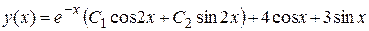
удовлетворяла этим начальным условиям.
Для этого найдем производную
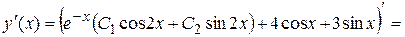
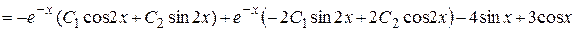 .
.
Вычислим 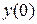 и
и 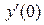 :
:
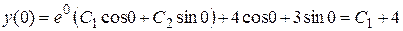 ,
,
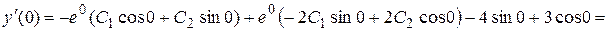
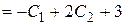 .
.
Подставим эти значения в равенства 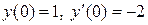 , получим
, получим
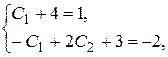 или
или 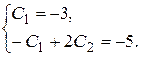
Получили систему уравнений относительно 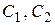 . Решая эту систему, находим
. Решая эту систему, находим 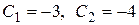 . Тогда искомое частное решение заданного дифференциального уравнения имеет вид
. Тогда искомое частное решение заданного дифференциального уравнения имеет вид
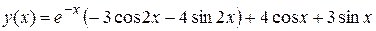 .
.
Ответ: 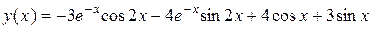 .
.
В некоторых случаях функция 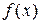 в правой части линейного неоднородного дифференциального уравнения не является функцией «специального вида», но может быть представлена в виде суммы таких функций. Тогда для отыскания частного решения
в правой части линейного неоднородного дифференциального уравнения не является функцией «специального вида», но может быть представлена в виде суммы таких функций. Тогда для отыскания частного решения 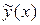 дифференциального уравнения можно использовать «принцип наложения», который заключается в следующем:
дифференциального уравнения можно использовать «принцип наложения», который заключается в следующем:
 Если в уравнении
Если в уравнении 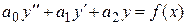 правая часть представляет собой сумму двух функций
правая часть представляет собой сумму двух функций 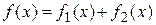 , а
, а 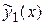 и
и 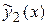 – частные решения уравнений
– частные решения уравнений
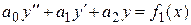 и
и 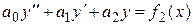
соответственно, то функция 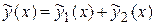 является частным решением исходного уравнения
является частным решением исходного уравнения 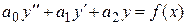 .
.
Рассмотрим пример.
Пример 9 Решить уравнение 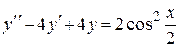 .
.
Решение
1) Найдем общее решение соответствующего однородного дифференциального уравнения:
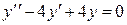 Þ
Þ 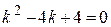 Þ
Þ 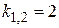 Þ
Þ 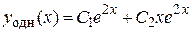 .
.
2) Найдем частное решение 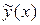 . Правая часть данного линейного неоднородного дифференциального уравнения не является функцией специального вида (смотри таблицу 4). Однако если преобразовать эту функцию:
. Правая часть данного линейного неоднородного дифференциального уравнения не является функцией специального вида (смотри таблицу 4). Однако если преобразовать эту функцию:
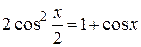 ,
,
то ее можно рассматривать как сумму функций 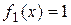 и
и 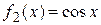 специального вида. Тогда частное решение исходного дифференциального решение исходного дифференциального уравнения также можно найти методом подбора частного решения, используя принцип наложения. Для этого рассмотрим два дифференциальных уравнения:
специального вида. Тогда частное решение исходного дифференциального решение исходного дифференциального уравнения также можно найти методом подбора частного решения, используя принцип наложения. Для этого рассмотрим два дифференциальных уравнения:
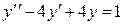 и
и 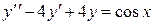
и найдем частное решение каждого из этих уравнений.
а) Для дифференциального уравнения 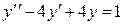 частное решение будем искать в виде
частное решение будем искать в виде
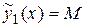 ,
,
так как 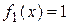 есть многочлен нулевой степени (число), а число
есть многочлен нулевой степени (число), а число 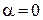 не является корнем характеристического уравнения (случай I,а таблицы 4). Найдем значение параметра М.
не является корнем характеристического уравнения (случай I,а таблицы 4). Найдем значение параметра М.
Имеем:
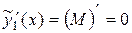 ,
, 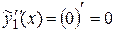 .
.
Подставим 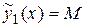 ,
, 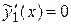 ,
, 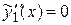 в дифференциальное уравнение
в дифференциальное уравнение 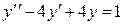 :
:
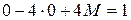 Þ
Þ 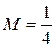 .
.
Тогда 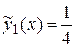 .
.
б) Частное решение 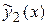 уравнения
уравнения 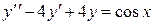 будем искать в виде
будем искать в виде
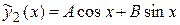 ,
,
так как 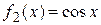 есть функция вида
есть функция вида 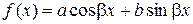 , где
, где 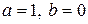 , а характеристическое уравнение не имеет комплексных корней (случай III,а таблицы 4).
, а характеристическое уравнение не имеет комплексных корней (случай III,а таблицы 4).
Для определения коэффициентов А и В находим
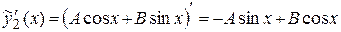 ,
,
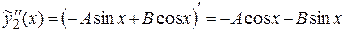 .
.
Подставляя эти производные и функцию 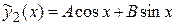 в дифференциальное уравнение
в дифференциальное уравнение 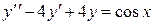 , получим
, получим
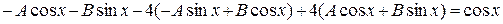 ,
,
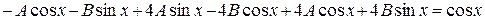 ,
,
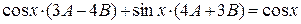 .
.
Приравнивая коэффициенты при одноименных функциях, получим систему уравнений относительно А и В:
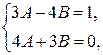
откуда находим 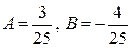 . Тогда
. Тогда 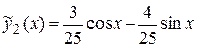 .
.
Следовательно, частное решение исходного дифференциального уравнения имеет вид
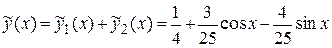 ,
,
а искомое общее решение –
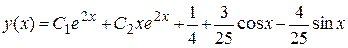 .
.
Ответ: 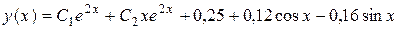 .
.
*) Напомним, что корни квадратного уравнения 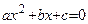 находят по формуле
находят по формуле 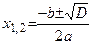 , где
, где 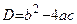 .
.
*) Количество линейно независимых функций ФСР равно порядку дифференциального уравнения
| <== предыдущая лекция | | | следующая лекция ==> |
| Аналитическая геометрия. Прямая и плоскость | | | Определение линейного пространства |
Дата добавления: 2017-11-21; просмотров: 1569;











