Обыкновенные дифференциальные уравнения.

Определение. Дифференциальное уравнение называется обыкновенным, если в нем одна независимая переменная; если же независимых переменных две или больше, то уравнение называется уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения.

Примеры.

1.x + yy ^/=0 – обыкновенное дифференциальное уравнении 1-го прядка.

2. 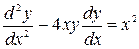- обыкновенное дифференциальное уравнение 2-го порядка.

3. 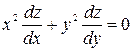- дифференциальное уравнение в частных производных 1-го порядка.

Рассмотрим обыкновенные дифференциальные уравнения.

Основная задача интегрального исчисления – отыскание функции y, производная которой равна данной непрерывной функции f(x), - сводится к простейшему дифференциальному уравнению

y ^/ = f(x).

Общее решение этого уравнения есть

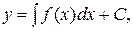
где С – произвольная постоянная, а под интегралом понимается одна из первообразных функции f(x).

Определение.Общим решением дифференциального уравнения 1-го порядка y ^/ = f(x,у) в области D называется функция y = φ(x, С), обладающая следующими свойствами:

1) она является решением данного уравнения при любых действительных значениях произвольной постоянной С;

2) для любого начального условия y(x₀) = y₀ такого, что (x₀,y₀) ? D, существует единственное значение С = С₀, при котором решение y = φ(x, С) удовлетворяет заданному начальному условию.

3) Всякое решение y = φ(x, С₀), получающееся из общего решения y = φ(x, С) при конкретном значении С = С₀, называется его частным решением.

Решим уравнение, полученное в задаче 1: 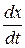= 2t + 3t²

x ^/(t) = 2t + 3t²

x (t) = 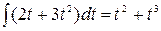+ C – общее решение дифференциального уравнения.

Используя начальные условия, найдем C. Так как x = 4 при t = 0, то подставив эти значения в общее решение, находим: С = 4.

Итак, закон движения тела имеет вид .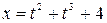

Задача Коши.

Задача в которой требуется найти частное решение уравнения y ^/ = f(x,у), удовлетворяющее начальному условию y(x₀) = y₀, называется задачей Коши.

Построенный на плоскости xOy график всякого решения y = φ(x) данного дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению y = φ(x, С) на плоскости xOy соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С.

Определение: График частного решения называется интегральной кривой рассматриваемого дифференциального уравнения.