Лекция 11 Знакоположительные ряды.

Числовой ряд называется знакоположительным, если все его члены – положительные (неотрицательные) числа.

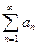
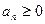
Основная и довольно приятная особенность знакоположительных рядов в том, что частичные суммы ряда представляют собой неубывающую последовательность.

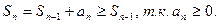
Поэтому достаточно проверить, что последовательность частичных сумм ограничена сверху, чтобы по теореме Вейерштрасса утверждать, что последовательность частичных сумм имеет конечный предел, т.е. ряд сходится.

На этом основаны, практически, все признаки сходимости рядов.

Ряд может сравниваться с несобственным интегралом (интегральный признак Коши), с другими рядами (признаки сравнения рядов), в частности, со сходящейся геометрической прогрессией (признак Даламбера, радикальный признак Коши).

Каждый признак можно сравнить с увеличительным стеклом. У каждого признака есть своя область применения, более широкая или более узкая (как поле зрения линзы) и своя сила. Одни признаки сильнее, позволяют различать слабо сходящиеся или слабо расходящиеся ряды, но имеют узкую область применения (например, интегральный признак Коши). Другие, наоборот, имеют широкую область применения, но довольно слабы, ряды, близкие к границе сходимости, с их помощью не различишь (например, признаки Даламбера и Коши (радикальный)).

Пока в библиотеке рядов, которые мы можем использовать для сравнения, всего два ряда: сходящийся ряд - бесконечно убывающая геометрическая прогрессия, известная еще из школы, и расходящийся гармонический ряд, полученный по критерию Коши.

Заметим, что критерий Коши (как критерий сходимости), вообще, самый сильный инструмент при исследовании сходимости ряда, но его область применимости узка.

Интегральный признак Коши, основанный на сравнении с несобственным интегралом – очень сильный признак. В самом деле, если аппроксимировать непрерывную подинтегральную функцию кусочно-постоянной, то площадь под графиком функции (интеграл) и площадь под графиком кусочно-постоянной функции будут различаться на конечное число.