Свойства сходящихся рядов.

1. Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.

Доказательство. Для второго ряда частичная сумма будет равна 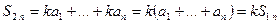. По теореме о предельном переходе в равенстве .

2. Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.

Сгруппируем члены ряда, например, так

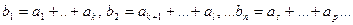. Видно, что частичные суммы группированного ряда представляют собой подпоследовательность последовательности частичных сумм исходного ряда. Так как последовательность сходится, то и подпоследовательность сходится к тому же пределу.

3. В сходящемся ряде можно отбросить конечное число первых членов 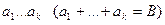. Полученный ряд будет сходиться, а его сумма будет меньше суммы исходного ряда на B.

Запишем частичные суммы второго ряда . По теореме о предельном переходе в равенстве .

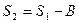Замечание. Ряд, полученный из исходного ряда отбрасыванием первых k членов, называется остатком ряда и обозначается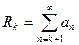

4. Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3).

Поэтому сходимость ряда можно исследовать, «начиная с некоторого n».

5. Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.

Рассмотрим два сходящихся ряда 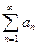и 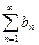. Рассмотрим ряд 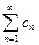, где . . 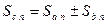Переходя к пределу в равенстве, получим .

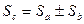Примеры.

1. Ряд –5+7-8+100+1+0,5+0,25+0,125+… сходится. В самом деле, отбросив первых четыре члена ряда (свойства 3,4), получим сходящуюся бесконечно убывающую геометрическую прогрессию

2. Ряд 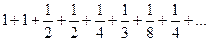расходится. Он представляет собой сумму двух рядов: сходящейся геометрической прогрессии (нечетные члены) и гармонического ряда (четные члены). Если бы этот ряд сходился, то, вычитая из него почленно сходящийся ряд 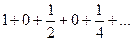, мы должны были бы по свойству 5 получить сходящийся ряд. А получаем расходящийся гармонический ряд. Следовательно, исходный ряд расходится.

3. Ряд 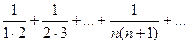сходится. Рассмотрим сходящийся ряд . Группируем его члены

, получаем исходный ряд. Следовательно, он сходится (свойство 2), и его сумма равна 1.