Лекция 10. Числовые ряды и их свойства.
Числовой ряд 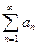 – это сумма бесконечного количества чисел, выбранных по определенному алгоритму. Обычно задают формулу общего члена ряда
– это сумма бесконечного количества чисел, выбранных по определенному алгоритму. Обычно задают формулу общего члена ряда 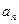 .
.
Примеры
1. 1+ 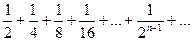 - бесконечно убывающая геометрическая прогрессия со знаменателем
- бесконечно убывающая геометрическая прогрессия со знаменателем 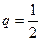 . Ее сумма равна
. Ее сумма равна 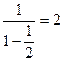 ,
,
2. 1+1+1+…..Сумма этого ряда бесконечна.
3. 1-1+1-1… Сумма этого ряда не существует (ни конечная, ни бесконечная).
При изучении рядов возникает основной вопрос: «Сходится ли ряд». Отвечая на этот вопрос для геометрической прогрессии, мы вычисляем последовательно 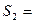 1+
1+ 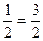 ,
, 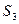 =1+
=1+ 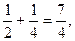
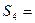 1+
1+ 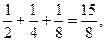 - суммы n членов ряда – частичные суммы ряда
- суммы n членов ряда – частичные суммы ряда 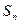 .
.
Ряд 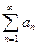 называется сходящимся,если существует конечный предел последовательности частичных сумм ряда – он называется суммой ряда
называется сходящимся,если существует конечный предел последовательности частичных сумм ряда – он называется суммой ряда
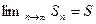 .
.
Рядназывается расходящимся, если предел частичных сумм ряда бесконечен или вообще не существует.
Необходимый признак сходимости ряда.Если ряд сходится, то 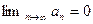 .
.
Доказательство. 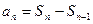 . Пусть ряд сходится, тогда
. Пусть ряд сходится, тогда 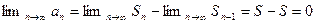 .
.
Необходимый признак позволяет отсеивать часть расходящихся рядов.
Достаточный признак расходимости.Если 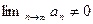 , то ряд расходится.
, то ряд расходится.
Доказательство (от противного). Пусть ряд сходится. Тогда по необходимому признаку сходимости ряда 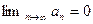 Противоречие с
Противоречие с 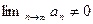 .
.
Пример. Ряд 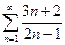 расходится, так как
расходится, так как 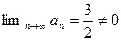
Пример Ряд 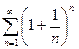 расходится, так как
расходится, так как 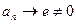 .
.
Дата добавления: 2017-11-21; просмотров: 1322;











