Свойства криволинейного интеграла первого рода.
1. Линейность
а) свойство суперпозиции 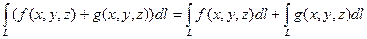
б) свойство однородности 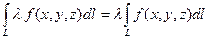 .
.
Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Так как в интегральной сумме число слагаемых конечно, перейдем к интегральным суммам для правых частей равенств. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.
2. Аддитивность.
Если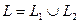 ,то
,то 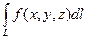 =
= 
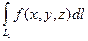 +
+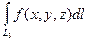
Доказательство. Выберем разбиение области L так, чтобы ни один из элементов разбиения ( первоначально и при измельчении разбиения) не содержал одновременно как элементы L1, так и элементы L2. Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1.
3. 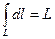 .Здесь
.Здесь 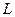 – длина дуги
– длина дуги 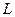 .
.
4. Если на дуге 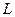 выполнено неравенство
выполнено неравенство 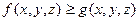 , то
, то 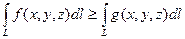
Доказательство. Запишем неравенство для интегральных сумм и перейдем к пределу.
Заметим, что, в частности, возможно 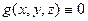
5. Теорема об оценке.
Если существуют константы 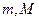 , что
, что 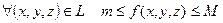 , то
, то
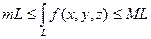
Доказательство. Интегрируя неравенство 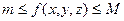 (свойство 4), получим
(свойство 4), получим 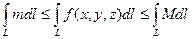 . По свойству 1 константы
. По свойству 1 константы 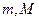 можно вынести из-под интегралов. Используя свойство 3, получим искомый результат.
можно вынести из-под интегралов. Используя свойство 3, получим искомый результат.
6. Теорема о среднем(значении интеграла).
Существует точка 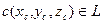 , что
, что 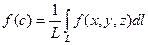
Доказательство. Так как функция 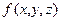 непрерывна на замкнутом ограниченном множестве
непрерывна на замкнутом ограниченном множестве 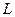 , то существует ее нижняя грань
, то существует ее нижняя грань 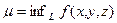 и верхняя грань
и верхняя грань 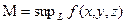 . Выполнено неравенство
. Выполнено неравенство 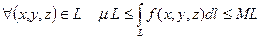 . Деля обе части на L, получим
. Деля обе части на L, получим 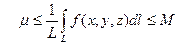 . Но число
. Но число 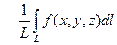 заключено между нижней и верхней гранью функции. Так как функция
заключено между нижней и верхней гранью функции. Так как функция 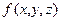 непрерывна на замкнутом ограниченном множестве L, то в некоторой точке
непрерывна на замкнутом ограниченном множестве L, то в некоторой точке 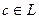 функция должна принимать это значение. Следовательно,
функция должна принимать это значение. Следовательно, 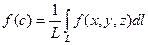 .
.
Дата добавления: 2017-11-21; просмотров: 1162;











