Задача о работе силы.

| Какую работу производит сила F(M) при перемещении точки M по дуге AB?
Если бы дуга AB была отрезком прямой, а сила была бы постоянной по величине и направлению при перемещении точки M по дуге AB, то работу можно было бы вычислить по формуле 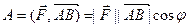 , где , где 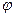 - угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги - угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги 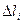 достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды 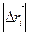 , так как эти величины – эквивалентные бесконечно малые величины при условии , так как эти величины – эквивалентные бесконечно малые величины при условии 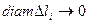 (первый семестр). (первый семестр).
|
1. Организуем разбиение области- дуги AB на элементы – элементарные дуги 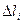 так, чтобы эти элементы не имели общих внутренних точек и
так, чтобы эти элементы не имели общих внутренних точек и 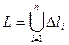 (условие А)
(условие А)
2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции 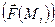
3. Построим интегральную сумму 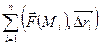 , где
, где 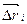 вектор, направленный по хорде, стягивающей -дугу
вектор, направленный по хорде, стягивающей -дугу 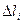 .
.
4. Переходя к пределу при условии 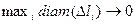 (условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы):
(условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы):
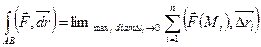 .Часто обозначают
.Часто обозначают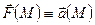
Дата добавления: 2017-11-21; просмотров: 1073;











