Задача о массе кривой. Криволинейный интеграл 1 рода.

Задача о массе кривой. Пусть в каждой точке кусочно-гладкой материальной кривой L: (AB) задана ее плотность 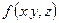. Определить массу кривой.

Поступим так же, как мы поступали при определении массы плоской области (двойной интеграл) и пространственного тела (тройной интеграл).

1. Организуем разбиение области- дуги L на элементы – элементарные дуги 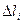так, чтобы эти элементы не имели общих внутренних точек и 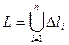(условие А)

2. Отметим на элементах разбиения «отмеченные точки» M_i и вычислим в них значения функции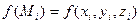

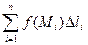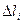3. Построим интегральную сумму , где - длина дуги 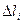(обычно вводятся одни и те же обозначения для дуги и ее длины). Это – приблизительное значение массы кривой. Упрощение состоит в том, что мы предположили плотность дуги постоянной на каждом элементе и взяли конечное число элементов.

Переходя к пределу при условии 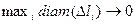(условие В), получим криволинейный интеграл первого рода как предел интегральных сумм:

.

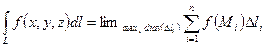Теорема существования[10].

Пусть функция 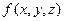непрерывна на кусочно-гладкой дуге L[11]. Тогда криволинейный интеграл первого рода существует как предел интегральных сумм.

Замечание. Предел этот не зависит от

- способа выбора разбиения, лишь бы выполнялось условие А

- выбора «отмеченных точек» на элементах разбиения,

- способа измельчения разбиения, лишь бы выполнялось условие В