Резонансное взаимодействие волн и частиц (квазилинейная теория)

<30 31 32 33 34 3536>

Плазму, в которой, в конце концов, возбуждается большое количество волн — мод колебаний (например, из-за неустойчивостей, рассмотренных ранее), можно назвать турбулентной, если амплитуды волн существенно превышают уровень тепловых флуктуации, а их фазы случайны. Вообще говоря, если уровень колебаний становится очень большим, то могут стираться описанные выше характерные черты отдельных мод. Поэтому специально выделяют более простой случай не очень больших амплитуд — так называемое приближение слабой турбулентности. Нелинейность плазмы приводит к взаимодействию между модами типа рассмотренной в предыдущем параграфе распадной неустойчивости, так что коэффициенты в разложении по собственным колебаниям становятся медленно меняющимися (в масштабе периода колебаний) функциями времени.

Важная особенность плазменной турбулентности, отличающая ее от турбулентности жидкости, связана с тем, что в плазме значительную, а иногда и доминирующую роль играет известный из предыдущих параграфов эффект резонансного взаимодействия волн с частицами. В старшем порядке по амплитуде поля такой эффект соответствует индуцированному излучению и поглощению волн частицами, скорости которых связаны с частотами и волновыми векторами волн черенковским условием (резонанс Ландау):

Здесь уместно доставить вопрос о том, как будет меняться функция распределения резонансных частиц по скоростям при излучении и поглощении волн. В этом случае основной эффект обратного воздействия волны на частицы заключается в захвате резонансных частиц волной и их фазовых осцилляциях в потенциальной яме. Зависимость периода фазовых колебаний от энергии частиц приводила к фазовому размешиванию, так что функция распределения в узком интервале скоростей испытывала мелкомасштабные осцилляции, сглаженная по этим осцилляциям функция распределения была постоянна вдоль траекторий.

Траектории резонансных частиц существенно отличались от невозмущенных, и решение задачи удалось получить только благодаря тому, что уравнения движения частиц при достаточно медленном изменении амплитуды волны имеют точные интегралы. Уже при наличии трех волн строгий анализ движения резонансных частиц становится безнадежно сложным, и аналитическое решение задачи для этого случая до сих пор не получено. Ситуация, однако, существенно упрощается в предельном случае очень большого числа волн, когда можно использовать статистический подход, считая случайными их фазы.

Действительно, предположим, что в плазме возбужден широкий пакет волн, фазовые скорости которых достаточно плотно заполняют некоторый интервал ,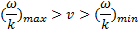

так что области захвата соседних волн перекрываются. Очевидно, что для этого должно быть выполнено условие

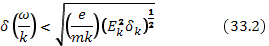
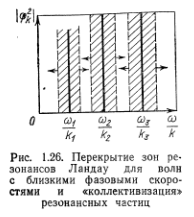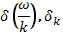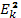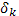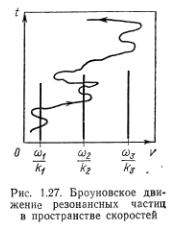
где — расстояние между соседними гармониками по фазовой скорости и волновому числу соответственно; — спектральная плотность энергии электрического поля плазменных шумов. Тогда энергия плазменных шумов на интервале равна , среднеквадратичный потенциал на этом интервале и условие (33.2) действительно соответствует перекрытию потенциальных ям для соседних волн (рис. 1.26). При выполнении этого условия происходит своеобразная «коллективизация» резонансных частиц между, двумя любыми соседними волнами. Если фазы волн случайны, то в результате толчков со стороны многих волн скорость частицы как бы участвует в броуновском движении. В фазовом пространстве это броуновское движение складывается со свободным движением частиц, так что результирующие траектории имеют вид, изображенный на рис. 1.27. С течением времени броуновские траектории частиц хаотически, но достаточно плотно заполняют на фазовой плоскости весь участок резонансных скоростей частиц: .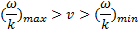

Относительно полной ширины пакета волн в этом случае «предполагается, что она существенно больше ширины потенциальной ямы, созданной пакетом:

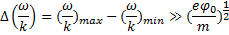(33.3)

где — среднеквадратичный потенциал в пакете волн. Устанавливающаяся в этих условиях функция распределения, разумеется, содержит мелкомасштабные шероховатости и сохраняет (в отсутствие столкновений) энтропию, но физический смысл имеет только сглаженная функция распределения, которая соответствует росту энтропии и описывает диффузию резонансных частиц в поле волны. В результате диффузии функция распределения будет выравниваться, т. е. стремиться к постоянному значению, на участке 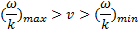, заполненном траекториями частиц (постоянство сглаженной функции распределения на траекториях имело место и в случае монохроматической волны).

Процесс диффузии резонансных частиц можно описать в рамках так называемого квазилинейного приближения. При получении уравнений этого приближения предполагается, что амплитуды возбужденных в плазме волн не слишком велики, так что нелинейными взаимодействиями между колебаниями можно пренебречь, а единственный нелинейный эффект, который принимается во внимание, связан с обратным воздействием колебаний на распределение резонансных частиц по скоростям, в результате чего возбуждение и поглощение колебаний происходят на медленно меняющемся под действием самих же колебаний «фоне».

Мы не будем вдаваться в детали обоснования уравнений квазилинейного приближения (хотя такое обоснование уже давно проведено), а ограничимся наиболее простым выводом этих уравнений для случая взаимодействия с плазмой ленгмюровских колебаний. Будем считать плазму однородной, а колебания одномерными.

В соответствии со сделанным выше замечанием функцию распределения резонансных частиц по скоростям представим в виде

Здесь 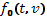—медленно меняющаяся функция распределения, характеризующая фон, на котором развиваются колебания; —осциллирующая в пространстве и во времени добавка к функции распределения, характеризующая эти колебания. Очевидно, что

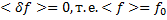
Скобки здесь означают усреднение по временному интервалу, большому по сравнению с периодом колебаний, и по пространственному интервалу, большому по сравнению с длиной волны.

Тогда уравнение для 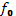получается простым усреднением исходного кинетического уравнения и имеет вид

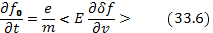
Здесь кроме соотношений (33.4) и (33.5) учтено отсутствие среднего электрического поля в плазме<Е>=0. Слагаемое, перенесенное в правую часть уравнения (33.6), определяет изменение 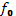из-за наличия среднеквадратичного эффекта быстрых осцилляции (так называемый квазилинейный интеграл столкновений). При получении его явного вида учтем, что в плазме возбужден достаточно широкий пакет волн, т. е.

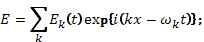
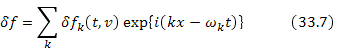
В этих формулах 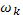— частоты линейных плазменных мод, определяемые соотношением 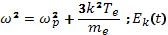—амплитуды этих мод, медленно меняющиеся со временем в результате взаимодействия с резонансными частицами. Поскольку величины 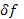и по физическому смыслу должны быть вещественны, то очевидно, что в разложениях (33.7) и гармоники комплексно сопряжены, т. е. выполняются условия:

Используя эти условия, уравнение (33.6) перепишем в виде

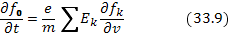
(гармоники с из этой суммы исчезают при усреднении).

Выше отмечалось, что эффектом нелинейного взаимодействия гармоник в квазилинейном приближении пренебрегается. Соответственно этому для связи 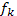и используем формулу линейной теории

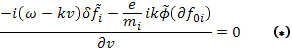
Единственное отличие от линейной теории состоит в том, что в этой формуле под 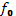понимается меняющаяся со временем фоновая функция распределения; формула (*) применима, если «фон» изменяется со временем достаточно медленно в масштабепериода колебаний .

Учитывая также, резонансный знаменатель 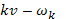в этой формуле следует понимать в смысле

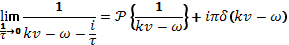
получаем окончательно следующую формулу для :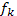

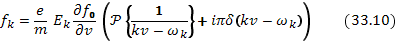
Подставляя 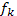в (33.9) и учитывая, что 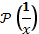—нечетная, а —четная функция аргумента, получаем следующее уравнение для :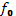

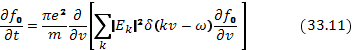
В правой части уравнения (33.11) можно перейти от суммирования к интегрированию по волновым числам с помощью соотношения 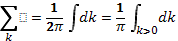. В этой формуле учтено, что элементарный «интервал» k, приходящийся на одно колебание, 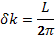(L —линейный размер плазмы, всюду для простоты полагается L=1). Формулы для случая 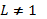получаются с помощью очевидной замены 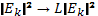. Выполняя в (33.11) интегрирование по k с помощью δ-функции, можно записать это уравнение в виде квазилинейного уравнения диффузии по скорости

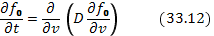
где коэффициент диффузии определяется спектральной плотностью плазменных шумов 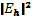в резонансной точке спектра :

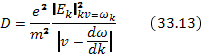
Разумеется, это уравнение диффузии следует дополнить уравнением для амплитуд волн, т. е. фактически для изменения со временем коэффициента диффузии. В квазилинейном приближении инкремент отдельной гармоники спектра совпадает с линейным

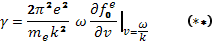
однако опять-таки под 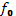в этой формуле следует понимать медленно меняющийся со временем «фон». В результате имеем систему

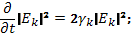
Уравнения (33.12) —(33.14) и есть замкнутая система уравнений квазилинейного приближения. С помощью этих уравнений ниже рассмотрены две простые задачи — о релаксации электронного пучка в плазме и о поглощении пакета плазменных колебаний.

Начнем с задачи о релаксации электронного пучка. Начальная функция распределения по скоростям для такой задачи имеет вид, показанный на рис. 1.28. 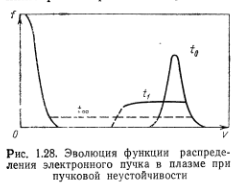Максимум функции распределения при 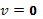соответствует тепловым частицам плазмы, имеющим, например, максвелловское распределение, второй максимум соответствует пучку быстрых (надтепловых) частиц. Если разброс по скоростям в пучке достаточно велик , то инкремент неустойчивости плазменных волн определяется из уравнения (**), релаксацию такого пучка можно рассматривать в рамках квазилинейных уравнений.

Если же электронный пучок первоначально моноэнергетический 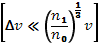, то на начальной стадии его релаксации происходит возбуждение монохроматической волны. Волна нарастает до значения — 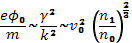и стабилизируется. При более детальном рассмотрении, однако, оказывается, что монохроматическая волна сама по себе неустойчива. Рано или поздно она размывается в пакет волн. Здесь этот процесс не рассмотрен. Важно лишь, что, в конце концов, дальнейшую релаксацию пакета снова можно рассматривать в квазилинейном приближении.

Таким образом, будем считать разброс по скоростям в пучке достаточно большим, так что применимы квазилинейные уравнения. Тогда волны с фазовыми скоростями в некотором интервале, где , оказываются неустойчивыми. Возбуждение волн сопровождается диффузией частиц пучка по скоростям, и в первоначальной области неустойчивости устанавливается «плато» на функции распределения (см. рис. 1.28). Однако такая функция распределения неустойчива, на ее переднем фронте производная положительна и происходит возбуждение волн. Область неустойчивости и соответственно область диффузии в пучке все время смещаются к меньшим скоростям. В результате на функции распределения возникает как бы волна релаксации, имеющая вид ступеньки с крутым фронтом и распространяющаяся в область малых скоростей. Перед фронтом шумы остаются на тепловом уровне, за фронтом возбуждены интенсивные плазменные шумы, и функция распределения близка к «плато». Процесс релаксации заканчивается, лишь когда частицы пучка продиффундируют до скоростей, сравнимых с тепловой скоростью плазмы. Окончательные границы «плато» определяются из следующих соотношений:

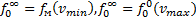(33.15)

Здесь —окончательная функция распределения в резонансной области, имеющая вид «плато» 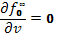; 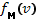— максвелловская функция распределения тепловых частиц плазмы;

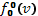—начальная функция распределения в пучке. Очевидно, что

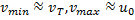(33.15а)

Высоту «плато» можно найти, воспользовавшись законом сохранения числа частиц в резонансной области:

(33.15б)

откуда имеем приближенно

Спектральную плотность энергии плазменных шумов в резонансной области найдем с помощью так называемого интеграла энергии квазилинейных уравнений. Для его получения подставим в правую часть квазилинейного уравнения диффузии 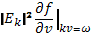из уравнения (33.14) для 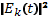. В результате приходим к следующему соотношению:

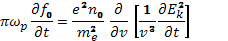
Проинтегрируем это уравнение по времени и пренебрежем вкладом тепловых шумов 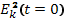. Интегрируя получившееся соотношение по скорости в пределах от 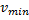до 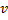с очевидным граничным условием — спектральная плотность шумов на границе резонансной области обращается в нуль 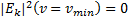, получаем искомый интеграл энергии — формулу, связывающую спектральную плотность плазменных шумов и изменение функции распределения резонансных частиц:

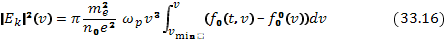
Как следует из формулы (33.16), спектральная плотность плазменных шумов вначале растет с ростом фазовой скорости, достигает максимума при 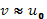и при больших скоростях быстро убывает, обращаясь в нуль при
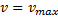(рис. 1.29). В той области скоростей, где первоначально не было пучка и 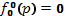( это и есть основная энергосодержащая область для спектра волн), из уравнения (33.16) имеем следующее соотношение для асимптотической формы спектра плазменных шумов, соответствующей «плато» на функции распределения по скоростям :

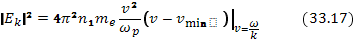
Полная энергия колебаний для такого спектра

Именно такую энергию теряет пучок при квазилинейной релаксации к состоянию с плато на функции распределения:

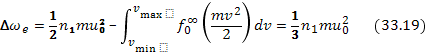
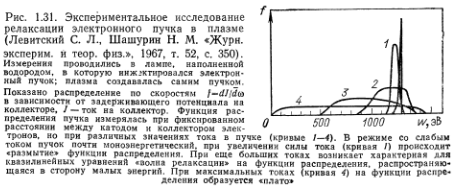
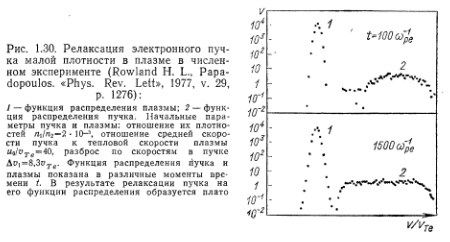Следует заметить, что спектр (33.16) —это еще неокончательно установившийся спектр в системе плазма — пучок. Он может меняться в результате нелинейного взаимодействия волн. Однако для не слишком энергичного пучка, когда энергия плазменных колебаний также достаточно мала, процесс дальнейшей нелинейной эволюции спектра (33.16) существенно более медленный по сравнению со временем его установления в рамках квазилинейных уравнений. На рис. 1.30 и 1.31 приведены результаты численного моделирования и лабораторного эксперимента, иллюстрирующие образование плато на функции распределения.

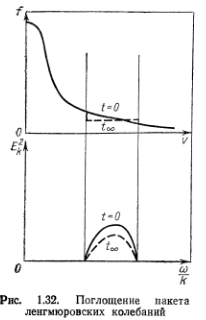Обратной по отношению к рассмотренной выше является задача о поглощении первоначально заданного пакета плазменных колебаний. Поглощение сопровождается диффузией резонансных частиц к большим скоростям и установлением «плато» на функции распределения (рис. 1.32). Спектр колебаний, устанавливающийся в результате такого процесса, можно найти из квазилинейного интеграла энергии, при выводе которого, естественно, уже нельзя пренебречь начальными колебаниями, и поэтому в уравнении (33.16) следует заменить 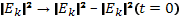. Долю энергии плазменных шумов, поглощаемых в плазме, легко можно оценить с помощью закона сохранения энергии:

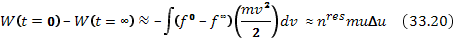
При малом числе резонансных частиц 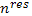только малая часть энергии волнового пакета поглощается в плазме, поглощение практически прекращается после установления «плато» на функции распределения резонансных частиц. В этих условиях дальнейшее поглощение плазменных колебаний возможно только при учете обычной столкновительной диффузии. Дело в том, что если квазилинейная диффузия приводит к установлению «плато» на функции распределения, 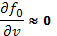, то столкновения стремятся вернуть наклон функции распределения к равновесному значению. В результате возникает конкуренция между влиянием волн и влиянием столкновений, при достаточно частых столкновениях функция распределения сильно отличается от вида «плато» и затухание Ландау сохраняется. Чтобы продемонстрировать это, введем в квазилинейное уравнение диффузии также и диффузионный член, соответствующий парным столкновениям. Для рассматриваемой задачи, в которой функция распределения существенно меняется лишь в узкой резонансной области, достаточно удержать только член со старшей производной 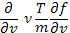, не учитывая динамического трения.

В результате конкуренции между квазилинейным воздействием волн на частицы и столкновениями в резонансной области должно установиться некоторое квазистационарное распределение 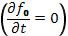, подчиняющееся уравнению

Интегрируя уравнение (33.21) один раз, находим

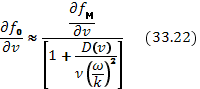
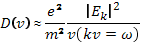коэффициент диффузии в резонансной области. Полученный наклон функции распределения подставим в формулу для декремента затухания . В результате

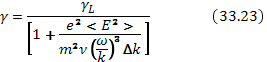
В этой формуле 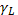— декремент затухания Ландау, рассчитанный по максвелловской функции распределения. Для достаточного пакета можно записать 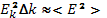, что и было сделано при выводе формулы (33.23).

Формулу (33.23) можно интерпретировать следующим образом. Запишем ее в виде

где 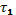— характерное время установления локального максвелловского распределения в резонансной области; 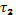— характерное время квазилинейной диффузии под действием волнового пакета. Если 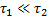, то столкновения успевают восстановить максвелловскую функцию распределения, и мы получим обычное затухание Ландау. В случае 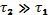функция распределения близка к «плато», и затухание стремится к нулю. На рис. 1.33 показаны результаты исследования аналогичного эффекта зависимости коэффициента усиления звука в решетке от амплитуды.

Отметим, что формула (33.24) применима и в случае поглощения монохроматической волны. В этом случае при выполнении условия 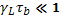фазовое размешивание резонансных частиц, захваченных в потенциальную яму, быстро «выключает» поглощение. Столкновения, также как и в случае пакета волн, восстанавливают максвелловское распределение резонансных частиц и затухание плазменной волны. Одновременный учет обоих факторов вновь приводит к формуле (33.24), где в данном случае 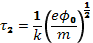— период фазовых колебаний захваченных частиц, определяющий время фазового размешивания, 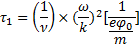—характерное время установления максвелловского распределения в области захвата .