Самосогласованное поле

Самое простое, что можно сделать для описания взаимодействия между частицами, — это вычислить силу F по средним значениям функции распределения, пренебрегая флуктуациями. При этом находится распределение частиц, создающее силовое поле, поддерживающее это самое распределение. Такое поле называется самосогласованным. С частным случаем самосогласованного электростатического поля мы уже встречались в теории электростатического экранирования Дебая.

Рассмотрим теперь более общий случай самосогласованного электромагнитного поля. Метод самосогласованного поля применим только к дальним взаимодействиям, так как на ближних взаимодействиях сильно сказываются флуктуации. Будем считать, что дальнодействующие силы в плазме имеют только электромагнитный характер. Тогда сила F, действующая на частицу с зарядом Ze, запишется как

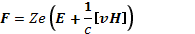(30.1)

Здесь подЕ и Н понимаются самосогласованные электрическое и магнитное поля, вычисляемые по уравнениям Максвелла, в которые подставляются плотности заряда q и тока j, найденные из усредненных функций распределения

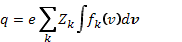(30.2)

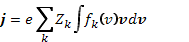(30.3)

Индекс k нумерует разные сорта частиц в плазме, включая электроны, которым приписывается Z = —1. Формулы (30.2) и (30.3) являются естественным обобщением формул (2.6) и (20.9) на многоскоростную задачу.

После подстановки выражения (30.1) в уравнение (29.4) система кинетических уравнений для плазмы принимает вид

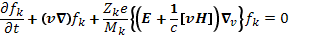(30.4)

Если поляЕ и Н находятся по уравнениям Максвелла с использованием выражений (30.2)—(30.3), то уравнение (30.4) будет называться кинетическим уравнением с самосогласованным полем или уравнением Власова.

Неточность метода самосогласованного поля заключается в пренебрежении флуктуациями (в частности, столкновениями), т. е. в замене средних значений функций функциями от средних значений. Такая замена вполне законна в линейном приближении по напряженностям полей. Отсюда следует, что метод самосогласованного поля является наиболее подходящим для линейной теории колебаний и волн в плазме.