Тензорные характеристики горячей плазмы и пространственная дисперсия

Рассмотрим теперь влияние газового давления на колебания плазмы в магнитном поле. Будем исходить из системы макроскопических уравнений (26.5) и (26.8) или (26.9), в которых уже опущены члены порядка отношения массы электрона к массе иона. Изменения состояния вещества в волне будем считать адиабатическими в термодинамическом смысле, что позволяет выразить градиенты давления через скорость звука. Для уравнения (26.5), описывающего движение плазмы как целого, градиент общего давления выражается через скорость ионного звука согласно формуле (27.19), после чего уравнение принимает вид

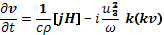(29.1)

Здесь u₃ — скорость ионного звука, выражаемая формулой (27.20). Для плоских волн уравнение (29.1) дает

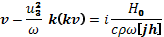(29.2)

где h — одиночный вектор в направлении магнитного поля. Здесь нам будет удобно выбрать ось х в направлении волнового вектора k. Направление оси z выберем так, чтобы магнитное поле лежало в плоскости xz. Выбранная система координат ориентирована по вектору k; мы будем называть ее k-системой в отличие от применяемой обычно H-системы, в которой ось z ориентирована по магнитному полю H.

В k-системе уравнение (29.2) позволяет выразить составляющие общей скорости плазмы в простом виде:

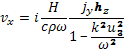(29.3)

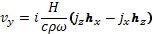(29.4)

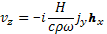(29.5)

Если магнитное поле направлено под углом θ к волновому вектору, то h_x = cosθ; h_z = sinθ; h_y = 0.

Составляющие электрического поля из уравнения электродинамики выражаются в k-системе формулами:

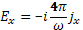(29.6)

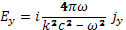(29.7)

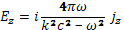(29.8)

Подстановка выражений (29.3)—(29.8) в векторное уравнение обобщенного закона Ома (26.9) дает систему линейных однородных алгебраических уравнений для составляющих плотности тока. Если приравнять нулю определитель этой системы, то можно получить дисперсионное уравнение. Мы проведем этот вывод в два приема: сначала подставим в обобщенный закон Ома выражения (29.3)—(29.5) для составляющих скорости и получим связь между электрическим полем и током, определяемую свойствами плазмы, которую можно выразить через тензор электрического сопротивления R:

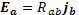(29.9)

Подставив затем в тензорное соотношение (29.9) составляющие электрического поля (29.6)—(29.8), получим систему однородных уравнений, дающую дисперсионное уравнение. Такой порядок вычислений позволяет выписать в явном виде тензор сопротивления плазмы, который может оказаться полезным.

Пренебрежем затуханием волн, т. е. вместо обобщенного закона Ома (26.9) воспользуемся уравнением идеальной проводимости (26.8). В этом уравнении градиент электронного давления выразим по формуле (27.16) через упорядоченную скорость электронов, которая в свою очередь может быть выражена через массовую скорость плазмы и плотность тока как

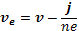
После этих подстановок уравнение (26.8) для плоской волны принимает вид

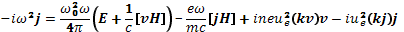(29.10)

Расписав это уравнение в составляющих, подставив для составляющих скорости выражения (29.3)—(29.5) и сравнив с выражением (29.9), получим тензор сопротивления горячей плазмы

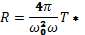(29.11)

гдекомпонентытензораТ* вk-системекоординат

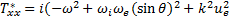
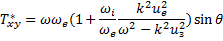
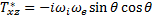
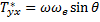
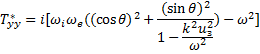(29.11a)

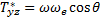
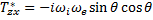
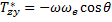
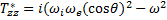
Если устремить скорости электронного и ионного звука к нулю, то получится тензор сопротивления холодной плазмы в k-системе. Связь между этими двумя представлениями тензора сопротивления легко получить из формул преобразования тензоров при повороте системы координат. Чтобы учесть конечную проводимость, достаточно, как видно из сопоставления уравнений (26.8) и (26.9), заменить в диагональных членах ω² на ω² + iωv, где v —эффективная частота столкновений.

Тензор сопротивления горячей плазмы можно получить и из микроскопических уравнений движения частиц (26.1)— (26.2). Запишем эти уравнения в общем виде для частицы с зарядовым числом Z и массой М как

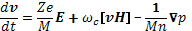(29.12)

где h — единичный вектор в направлении магнитного поля. Перейдем к плоской волне и выразим градиенты давления через скорости звука и согласно выражениям (27.15)— (27.16). Введем для каждого сорта частиц тензор частичного электрического сопротивления R_k и выразим его через вспомогательный тензор T_k

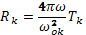(29.13)

Тензор частичного сопротивления выражается проще в H-системе координат, в которой ось z направлена вдоль магнитного поля. В этой системе координат вспомогательный тензор для каждого сорта частиц выражается как

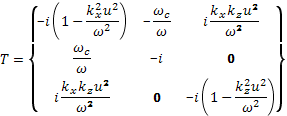(29.14)

Здесь u — скорость звука для частиц данного сорта. Обращением матрицы тензора Т_k можно получить тензор Т_k^-1и тензор полного сопротивления

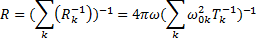(29.15)

Здесь суммирование производится по всем сортам частиц, присутствующих в плазме.

Мы не будем проводить довольно громоздкие выкладки. Если перейти в k-систему координат посредством поворота осей, то окончательное выражение для тензора сопротивления будет отличаться от выражения (29.11) только величинами порядка rn/М, опущенными при выводе макроскопических уравнений.

От тензора сопротивления легко перейти к тензорам проводимости σ и электрической проницаемости ε горячей плазмы:

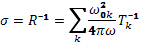(29.16)

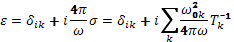(29.17)

Важнейшая особенность тензора электрической проницаемости горячей плазмы заключается в том, что он явным образом зависит не только от частоты, но и от волнового вектора. Последняя зависимость носит название пространственной дисперсии. Она является следствием теплового движения, приводящего к прямому переносу частиц из одной точки пространства в другую. Как видим, это свойство теплового движения проявляется уже в гидродинамическом приближении. Пространственная дисперсия сильно усложняет теорию колебаний горячей плазмы.

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 5, §§1-4)