Методы исследования устойчивости

Существуют три стандартных метода, обычно используемых для исследования устойчивости или свойств неустойчивостей, связанных с данным равновесным состоянием плазмы.

Простейший из них —интуитивный подход, согласно которому равновесное состояние подвергается возмущению, изменяющему силы, действующие на плазму. Если эти измененные силы действуют так, что увеличивают первоначальное возмущение, плазма неустойчива. Примером применения интуитивного подхода служит анализ змейковой неустойчивости. Этот подход не позволяет получить количественную информацию об инкрементах, однако с его помощью удается вскрыть механизм неустойчивости, показать, какие равновесные ситуации требуют дальнейшего анализа, а также получить информацию о том, какие моды, по-видимому, должны быть неустойчивыми.

Второй метод основан на энергетическом принципе. Равновесное состояние плазмы с потенциальной энергией W устойчиво, если W представляет собой минимальное значение, и неустойчиво в противном случае. Для исследования устойчивости плазмы этим методом необходимо вычислить изменение потенциальной энергии плазмы в результате данного возмущения. Плазменное равновесие устойчиво, если изменение потенциальной энергии положительно при любых возмущениях, не противоречащих уравнениям плазмы. Если же существует хотя бы одно допустимое возмущение, для которого приращение потенциальной энергии отрицательно, плазма неустойчива. Этот метод удобен при определении равновесных параметров в случае неустойчивого равновесия. Он не пригоден для нахождения инкремента конкретной неустойчивости.

Третий метод исследования устойчивости равновесия плазмы — анализ собственных частот. В этом методе предполагается, что, если исследуемое равновесное состояние подвергнуто возмущению, линеаризованные уравнения плазмы, описывающие развитие возмущения во времени, могут быть решены при соответствующих граничных условиях в предположении временной зависимости вида 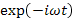. При этом мы получаем уравнение дляω, в которое входят равновесные параметры. Решения этого уравнениямогут быть действительными, мнимыми или комплексными. Если все решения дляω действительны, то любые переменные, описывающие возмущение, осциллируют гармонически и плазма устойчива. Если хотя бы одно из решений дляω имеет положительную мнимую часть, система неустойчива, поскольку соответствующее собственное колебание будет раскачиваться со временем.

Анализ собственных частот позволяет получить полную информацию о неустойчивостях, присущих конкретному равновесному состоянию плазмы. Развитие любого начального возмущения может быть прослежено до того предела, до которого справедливы линеаризованные уравнения. К сожалению, анализ собственных частот может быть применен лишь в тех случаях, когда равновесное состояние плазмы достаточно простое, чтобы дифференциальные уравнения плазмы могли быть решены для каждой из гибридных частот. Уменьшение показателя преломления с возрастанием частоты называется в оптике аномальной дисперсией, причем в наиболее характерных случаях аномальной дисперсии это уменьшение происходит резко, в узком интервале частот. Именно поэтому гибридные частоты и следует называть частотами аномальной дисперсии.

(источник:Н.Кролл, А.Трайвелпис, Основы физики плазмы, гл.5, §§1-3)