Кинетическая теория плазменных волн

В качестве простейшего примера применения метода самосогласованного поля рассмотрим высокочастотные линейные продольные колебания плазмы без внешнего магнитного поля. Для высокочастотной ветви движением ионов можно пренебречь. Поскольку движутся только электроны, уравнение Власова принимает вид

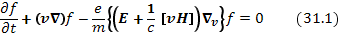
В линейном приближении записываем функцию распределения как сумму основной функции 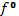и малого возмущения 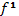. Функция 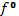является равновесной по отношению к рассматриваемому колебательному процессу. Но она вовсе не обязательно должна отвечать состоянию полного термодинамического равновесия. В разреженной плазме очень часто именно отступления от термодинамического равновесия приводят к колебательной неустойчивости, т. е. раскачке колебаний, установление же полного равновесия происходит только в процессе весьма медленной диссипации энергии возникающих колебаний. Поэтому мы будем считать функцию 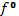не обязательно равновесной (как это часто делают), новообще некоторым фоном, на котором происходят колебания. Пусть колебания происходят на однородном фоне; тогда функция 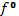постоянна в пространстве и во времени и является заданной функцией скоростей. В этих предположениях из уравнения (31.1) получается уравнение первого приближения для определения функции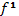

где 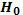— внешнее магнитное поле; 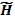— собственное магнитное поле волны. Рассмотрим плоскую волну вида 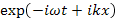. Согласно уравнению Максвелла

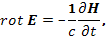
переменное магнитное поле происходит только от вихревого электрического поля. В плоской продольной волне электрическое поле безвихревое ( зависит только от x). Следовательно, при отсутствии внешнего магнитного поля собственное магнитное поле волны отсутствует и уравнение (31.2) принимает вид

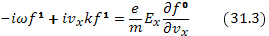
Электрическое поле находим из уравнения Максвелла и выражения (30..2):

Поскольку мы не вводили внешнего электрического поля 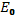, функция 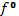должна давать нулевую плотность заряда.

Для получения дисперсионного уравнения следует выразить из уравнения (31.3) 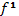через 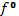и подставить в уравнение (31.4). Согласно уравнению (31.3),

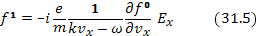
Подстановка в уравнение (31.4) дает

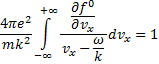
Это и есть дисперсионное уравнение, связывающее и 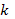. В общем случае оно оказывается трансцендентным, что характерно вообще для кинетической теории колебаний плазмы. В дальнейшем индекс 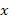при составляющей скорости будем опускать.

Удобно ввести нормированную основную функцию распределения f, определенную соотношением

где 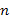— полная концентрация электронов. Нормированная функция распределения удовлетворяет условию

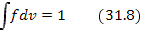
С помощью нормированной функции распределения дисперсионное уравнение плазменных волн можно записать в виде

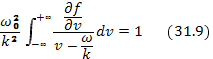
где 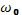— электронная плазменная частота. Для того чтобы интеграл (31.8) сходился, функция распределения на пределах интегрирования должна обращаться в нуль. Воспользовавшись этим, можно преобразовать интеграл в левой части уравнений (31.6) или (31.9) интегрированием по частям как

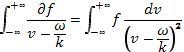
после чего дисперсионное уравнение принимает вид

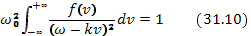
Заметим, что дисперсионное уравнение можно представить и еще в одной совершенно равноценной форме. Для этого достаточно умножить подынтегральную функцию в левой части уравнения (31.9) на величину

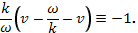
После этого интеграл примет вид

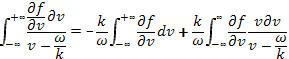
Первый интеграл в силу условия 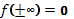обращается в нуль. Таким образом, уравнение (31.9) или (31.10) можно записать также и в форме

Эквивалентность уравнений (31.9) и (31.9а) означает, что составляющая скорости частиц вдоль направления распространения, усредненная по подынтегральной функции уравнения (31.9), равна фазовой скорости волны

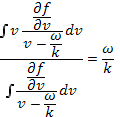
независимо от конкретного вида функции f, лишь бы она удовлетворяла условию интегрируемости, т. е. обращалась в нуль на бесконечности. Если это условие не выполнено, то интегралы теряют смысл.

Приближенное решение дисперсионного уравнения легко получить для случаев, когда функция распределения f быстро спадает с возрастанием скорости и при фазовой скорости 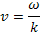уже достаточно мала. Если это так, то подынтегральная функция заметно отличается от нуля только в двух областях: при малых скоростях и вблизи особой точки 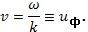Интеграл можно, таким образом, разбить на две част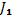и и отвечающие двум указанным областям.

Интеграл по области малых скоростей находится посредством разложения подынтегральной функции по степеням малой в этой области величины

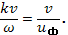
При этом удобно исходить из дисперсионного уравнения в форме (31.10), записав его как

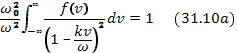
и разложив величину 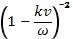в биноминальный ряд:

После этого преобразования интеграл по малым скоростям выразится как

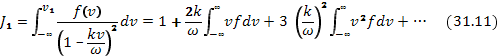
где 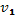— точно не определенное значение скорости, при котором функция распределения уже пренебрежимо мала, но которое еще меньше, чем фазовая скорость 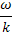. Интегралы в правой части уравнения (31.11) сходятся только при условии, если с возрастанием 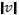функция распределения 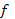спадает быстрее, чем любая степень скорости. Для равновесной максвелловской функции это условие выполнено, так как она спадает экспоненциально. Будем считать, что имеются только токи, связанные с самой волной, т. е. что сторонние токи отсутствуют, тогда первый интеграл в правой части уравнения (31.11) равен нулю. Если колебания происходят на изотропном фоне, то f (v) — четная функция и в уравнении (31.11) остаются только интегралы с четными степенями скорости

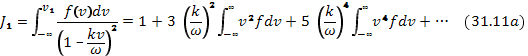
Перейдем к вычислению интеграла по области вблизи особой точки: 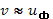. Этот интеграл удобнее вычислять исходя из дисперсионного уравнения в форме (31.9), где особая точка представляет собой простой полюс. Запишем интеграл в виде

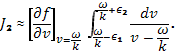
Этот интеграл несобственный, непосредственное интегрирование дает результат:

который зависит от выбора 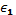и 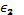и при устремлении этих величин порознь к нулю не стремится ни к какому определенному значению. Кроме того, в теории функций комплексного переменного логарифм является многозначной функцией, которая и при действительном аргументе может иметь мнимую часть.

Действительная часть интеграла приобретает определенное значение, если положить 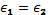. Это значение называется главным значением интеграла. Если вблизи точки 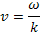значение близко к нулю, то главное значение интеграла пренебрежимо мало.

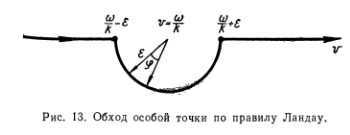
Для нахождения мнимой части интегрирование выполняется в комплексной плоскости. Здесь можно выбрать контур интегрирования, обходящий особую точку по полуокружности (рис. 13). Направление обхода определяется правилом Ландау, о котором речь будет ниже. На этой полуокружности

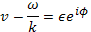
и интеграл сводится к

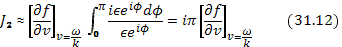
независимо от значения 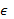, которое можно устремить к нулю. Этот результат можно было бы получить и непосредственно из теоремы вычетов, согласно которой интеграл по половине замкнутого контура, обходящего особую точку, равен 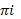, умноженному на вычет, который в данном случае равен просто числителю подынтегральной функции. Подстановка значени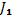й и в уравнения (31.10) и (31.9) дает дисперсионное уравнение в виде

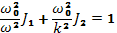
или после подстановки значений (31.11) и (31.12), ограничиваясь низшими степенями ,

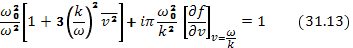
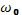Но в этом приближении и при малом затухании мало отличается от . Следовательно, результат (31.13) можно записать приближенно как

где 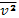— квадрат скорости движения в одном направлении, усредненный по функции f. Если представить комплексную частоту в виде

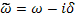
где 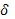— декремент затухания, то

Из результата (31.14) для вещественной и мнимой частей получится (считая 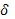малой величиной)

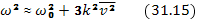
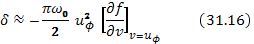
Где 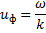— фазовая скорость волны. При принятой нами записи плоской волны в виде 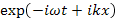зависимость от времени выражается множителем

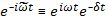
Следовательно, положительные значения 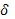отвечают затуханию, отрицательные — раскачке колебаний. Если функция распределения f уменьшается при возрастании абсолютного значения скорости, то мнимый член приводит к затуханию колебаний. Раскачка получится в том, и только в том случае, когда у функции распределения имеется «горб» при скоростях частиц, близких по величине и направлению к фазовой скорости волны.

Таким образом, мнимый член формулы (31.13) описывает затухание плазменных волн при отсутствии столкновений между частицами, которое называется затуханием Ландау. Оно является простейшим примером диссипации без столкновений — важнейшего явления в кинетике разреженной плазмы. Из формул (31.14) или (31.16) видно, что этот эффект происходит от наличия в плазме частиц, движущихся со скоростями, близкими к фазовой скорости волны, т. е. находящихся в фазовом резонансе с волной. На такие частицы электрическое поле волны действует все время почти в одной фазе, т. е. они наиболее тесно взаимодействуют с волной. Частицы, движущиеся немного медленнее фазовой скорости волны, отбирают у нее энергию; частицы, движущиеся немного быстрее, передают свою энергию волне, Затухание происходит тогда, когда преобладают частицы, слегка отстающие от волны, раскачка — когда преобладают слегка обгоняющие, что и выражается формулой (31.16).

В реальном случае трехмерного движения под 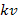следует понимать скалярное произведение 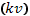, и условие фазового резонанса принимает вид . Это значит, что составляющая скорости частицы в направлении волнового вектора равна фазовой скорости волны. Для частицы, скорость которой больше фазовой скорости волны, всегда найдется такой угол, при котором это условие выполняется.

Затухание или раскачка плазменных волн при фазовом резонансе с частицами может рассматриваться как проявление эффекта Вавилова — Черенкова — поглощения или испускания волн частицами, движущимися со скоростью порядка или выше фазовой скорости волны в среде. Соответственно эти явления называют иногда черенковским затуханием (или возбуждением) колебаний. Следует отметить, что знак мнимого члена в формуле (31.14) зависит от направления обхода контуром интегрирования особой точки. Поэтому приведенный вывод является по существу нестрогим. Строгое рассмотрение показывает, что при наличии теплового движения плазменные колебания не имеют в точности вида плоских волн, а лишь асимптотически к нему стремятся. Для асимптотического решения получается дисперсионное уравнение, совпадающее с полученным выше, но знак мнимого члена оказывается уже определенным. Он дается правилом обхода Ландау, согласно которому, если плоская волна записана в виде 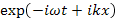, тo особая точка должна обходиться против часовой стрелки, т. е. снизу, как это и было сделано выше.

Применим теперь полученные результаты к случаю, когда колебания происходят вокруг состояния термодинамического равновесия, т. е. 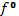есть функция распределения Максвелла

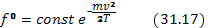
Где 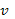— составляющая скорости в одном направлении; 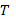— температура в энергетических единицах. Нормированная функция распределения

Усреднение квадрата скорости движения в одном направлении дает

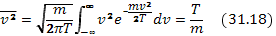
Формулы (31.15) и (31.16) для равновесной термической плазмы принимают вид

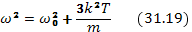
Последнюю формулу удобно преобразовать так, чтобы была явно видна зависимость затухания от волнового числа. Для этого воспользуемся тем, что формула применима лишь при частотах, близких к плазменной, откуда

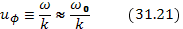
и введем дебаевскую длину 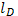, определенную как

Теперь формулу (31.20) можно записать в виде

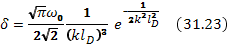
Таким образом, если длина волны меньше дебаевской, то затухание происходит за время порядка периода колебаний. Напротив, для длинных волн затухание экспоненциально мало. Но частота длинных волн близка к плазменной, что и оправдывает сделанные при выводе приближения.

Действительная часть дисперсионного уравнения (31.19) совпадает с гидродинамическим приближением 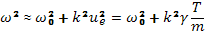, если показателю адиабаты приписывать значение

отвечающее движению в одном направлении.

(источник:Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 6, §§7-8)