Магнитогидродинамические волны
Рассмотрим теперь волны, распространяющиеся в плазме вдоль магнитного поля, при произвольном направлении поляризации. Как показано выше, такую волну можно разложить на две независимые волны, у одной из которых электрическое поле параллельно, у другой —перпендикулярно к магнитному. Волна, у которой как направление распространения, так и направление поляризации параллельны магнитному полю, в холодной плазме вырождается в плазменные колебания фиксированной частоты ω=ω0. Перейдем теперь к волне, распространяющейся вдоль магнитного поля, но поляризованной поперек него. Для этой волны
(kЕ)=0 (23.1)
и уравнение (20.5) сводится к виду
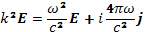 (23.2)
(23.2)
Допустим, что током смещения, т. е. членом (ω2/c2) Е, можно пренебречь. Для этого нужно, чтобы показатель преломления плазмы был велик
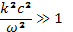 (23.3)
(23.3)
Условия применимости этого допущения мы проверим ниже. Если условие (23.3) выполнено, то вместо уравнения (23.2) можно написать
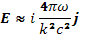 (23.4)
(23.4)
Из уравнения (23.2) видно, что ток параллелен электрическому полю, т. е. для рассматриваемых волн перпендикулярен к магнитному. Следовательно, уравнение (20.18) принимает вид
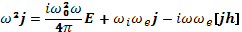 (23.5)
(23.5)
что после подстановки выражения (23.4) дает
 (23.6)
(23.6)
Последний член справа показывает, что по отношению к рассматриваемым волнам замагниченная плазма обладает своеобразной анизотропией: свойства волны зависят от того, образуют ли векторы k, jиh правую или левую тройку. Среды с подобными свойствами называются гиротропнsми. Кроме плазмы к ним относятся, например, ферриты, широко используемые в радиотехнике.
Рассмотрим сначала предельную область очень низких частот
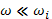 (23.7)
(23.7)
В этой области членами, содержащими ω2 и ωωe, можно пренебречь в сравнении с членом, содержащим ωiωe, вследствие чего гиротропные свойства плазмы не проявляются. Из уравнения (23.6) для этого предельного случая получается простое дисперсионное уравнение
 (23.8)
(23.8)
откуда квадрат показателя преломления
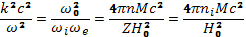 (23.9)
(23.9)
и фазовая скорость волны
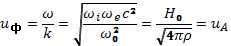 (23.10)
(23.10)
где ρ — плотность плазмы,
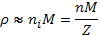 (23.11)
(23.11)
Скорость распространения, выражаемая формулой (23.10), называется альфвеновской скоростью, а сами волны— альфвеновскими или магнитогидродинамическими. Квадрат альфвеновского показателя преломления (23.9) равен значению поперечной диэлектрической проницаемости плазмы, которое мы получили выше при рассмотрении поляризационного дрейфа. Предельная область (23.7) полностью описывается уравнениями магнитной гидродинамики, и формулу (23.10) легко получить из модели идеально проводящей жидкости. Для этого достаточно написать линеаризованное уравнение движения
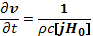 (23.12)
(23.12)
или
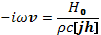 (23.13)
(23.13)
Если выразитьj через Е из формулы (23.4), то это уравнение переходит в
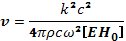 (23.14)
(23.14)
Далее используется условие идеальной проводимости
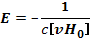 (23.15)
(23.15)
и дляЕ⊥Н0 получается дисперсионное уравнение
 (23.16)
(23.16)
откуда для фазовой скорости следует значение по формуле (23.10). Условие (23.15) обеспечивает вмороженность магнитного поля. Отсюда можно понять физическую картину магнитогидродинамических волн. Они могут рассматриваться как поперечные колебания силовых линий вместе с плазмой, в которую они вморожены, наподобие упругих колебаний струны. В области низких частот, удовлетворяющих условию (23.7), магнитогидродинамические волны распространяются с постоянной скоростью, т. е. дисперсия отсутствует и групповая скорость равна фазовой. Чтобы наряду с условием (23.7) выполнялось также и неравенство (23.3), т. е. альфвеновский показатель преломления был велик, требуется, согласно выражению (23.9),
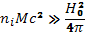 (23.17)
(23.17)
т. е. магнитная энергия плазмы должна быть мала в сравнении с энергией покоя. При малой плотности плазмы или очень сильном магнитном поле это условие может не выполняться. В этих случаях простое дисперсионное уравнение (23.16) должно быть заменено несколько более сложным соотношением.
Дата добавления: 2021-10-28; просмотров: 498;











