Волны в плазме без магнитного поля

Если магнитноеполе отсутствует, то 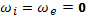и уравнение (20.18) сводится к виду

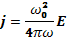(21.1)

После этого из выражения (20.5) получаем

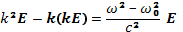(21.2)

Произвольную волну в плазме без магнитного поля можно разложить на две независимые волны: продольную (k || E) и поперечную (k ┴E). Для продольной волны k(kЕ)=k²E и из выражения (21.2) получим

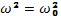(21.3)

Это уже знакомые нам электростатические плазменные колебания, которые в случае холодной плазмы возможны только на фиксированной плазменной частоте. Для поперечных волн (kЕ) = 0 и уравнение (21.2) дает

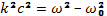(21.4)

Это — дисперсионное уравнение для распространения электромагнитных волн в плазме без магнитного поля. Распространение возможно только при частотах выше плазменной. Для ω²<ω₀² волновое число и показатель преломления становятся мнимыми, т. е. волна отражается от границы плазмы. Фазовая скорость

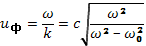(21.5)

В области, где фазовая скорость вещественна (ω²>ω₀²), она всегда больше скорости света и при приближении к плазменной частоте стремится к бесконечности. Групповая скорость находится дифференцированием формулы (21.4)

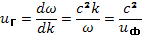(21.6)

откуда

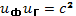(21.7)

Групповая скорость всегда меньше скорости света. При частотах гораздо больше плазменной как фазовая, так и групповая скорости стремятся к скорости света: волна распространяется, как в пустоте. При стремлении частоты волны к плазменной частоте фазовая скорость стремится к бесконечности, а групповая скорость — к нулю.