Кулоновские поправки к свободной энергии и давлению плазмы

Как известно из статистической термодинамики, энергия ℰ и свободная энергия F выражаются через статистическую сумму Σ формулами:

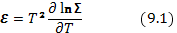
Здесь по принятому условию температура выражена в энергетических единицах, т. е. постоянная Больцмана положена равной единице. Формула (9.1) позволяет выразить статистическую сумму через энергию в виде неопределенного интеграла

Подстановка в формулу (9.2) дает выражение для свободной энергии

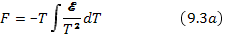
Тот же результат легко получить и из формальной термодинамики интегрированием уравнения Гиббса — Гельмгольца

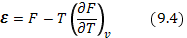
Если энергия аддитивна, т. е. представляется суммой нескольких членов, то в силу линейности приведенных формул они справедливы для каждого члена в отдельности. Давление

s New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t> (9.5)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">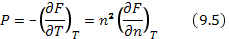

Согласно формуле (8.6) кулоновская энергия, отнесенная к одной частице,

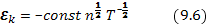
В этом случае в выражении (9.3) за нижний предел интегрирования можно принять то значение температуры, при котором энергия обращается в нуль, т. 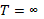. После этого выражение (9.3а) дает для кулоновской поправки к свободной энергии

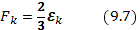
или, после подстановки формулы (8. 9),

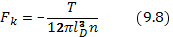
Для кулоновской поправки к давлению (9.5) получим

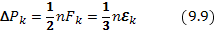
Эта поправка всегда отрицательна. Выведенными формулами исчерпывается вопрос о кулоновских поправках к термодинамическим функциям и к уравнению состояния плазмы в приближении Дебая.