Составление уравнений характеристик простых трубопроводов
Если трубопровод не имеет разветвлений и состоит из ряда последовательно включенных элементов, то он называется простым трубопроводом. Если же в трубопроводе есть хотя бы одно разветвление, то его называют сложным.
Составление уравнений характеристик простых трубопроводов (участков 1, 2, 3 и 4) базируется на заданном условии: на участках 1 и 4 – режим течения турбулентный, а на участках 2 и 3 – ламинарный.
Под характеристикой трубопровода понимается зависимость потерь давления в трубопроводе от расхода. Потери делят на потери на трение по длине трубы и потери в местных сопротивлениях (местные потери)
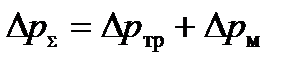 . (2.23)
. (2.23)
Потери на трение в трубе длиной 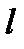 и внутренним диаметром
и внутренним диаметром 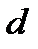 определяются по формуле Дарси-Вейсбаха
определяются по формуле Дарси-Вейсбаха 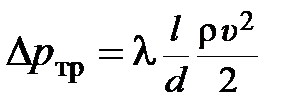 , которая при замене скорости объёмным расходом принимает вид
, которая при замене скорости объёмным расходом принимает вид
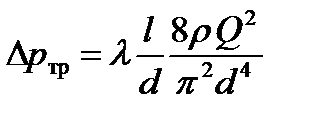 , (2.24)
, (2.24)
или для напора
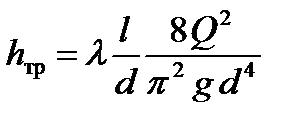 ,
,
При ламинарном режиме течения (Re< 2300) 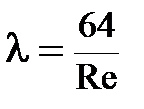 и формула Дарси преобразуется в формулу Пуазейля
и формула Дарси преобразуется в формулу Пуазейля
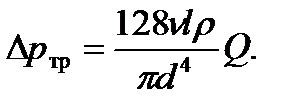 (2.25)
(2.25)
Местные потери могут быть заданы следующим образом:
- коэффициентом местного сопротивления 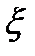 и тогда зависимость потерь от расхода выразится формулой, получаемой при замене скорости в уравнении Вейсбаха
и тогда зависимость потерь от расхода выразится формулой, получаемой при замене скорости в уравнении Вейсбаха
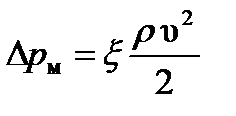 ,
,
расходом,
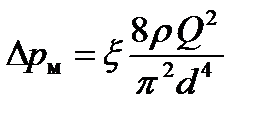 , (2.26)
, (2.26)
- площадью проходного сечения отверстия в местном сопротивлении 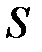 и коэффициентом расхода этого отверстия
и коэффициентом расхода этого отверстия 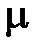 и в этом случае потери выражаются из формулы истечения
и в этом случае потери выражаются из формулы истечения
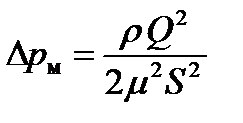 , (2.27)
, (2.27)
- эквивалентной длиной 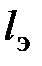 , при этом считается, что потери в местном сопротивлении эквивалентны потерям в трубе длиной
, при этом считается, что потери в местном сопротивлении эквивалентны потерям в трубе длиной 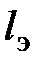 , и тогда для ламинарного режима течения при определении потерь используется формула
, и тогда для ламинарного режима течения при определении потерь используется формула
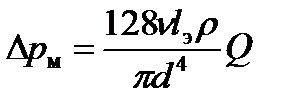 . (2.28)
. (2.28)
Формулы (7), (8) и (9) можно представить в следующем виде:
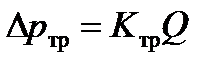 ,
, 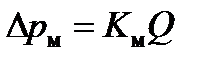 или
или 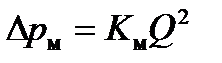 .
.
В общем случае характеристика простого трубопровода, не содержащего гидродвигатель, может быть представлена в виде
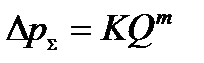 . (2.29)
. (2.29)
В схему любого объёмного гидропривода входит гидродвигатель устройство, преобразующее энергию потока рабочей жидкости в механическую работу на его выходном звене. При гидродинамическом расчёте гидродвигатель рассматривается как некоторое специальное местное гидравлическое сопротивление, в котором потери давления ( 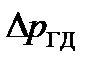 ) идут на совершение полезной работы – перемещение выходного звена, преодолевающего внешнюю нагрузку.
) идут на совершение полезной работы – перемещение выходного звена, преодолевающего внешнюю нагрузку.
Поэтому уравнение характеристики простого трубопровода (5), содержащего гидродвигатель, можно представить в виде
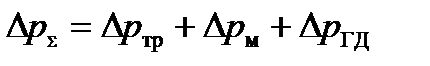 ,
,
а уравнение (2.29) в виде
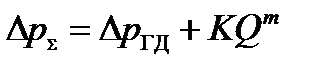 . (2.30)
. (2.30)
Определение величины 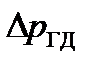 зависит от типа гидродвигателя. Самыми распространенными гидродвигателями являются гидромотор, в котором выходное звено совершает вращательное движение, и гидроцилиндр –гидродвигатель с возвратно-поступательным движением выходного звена.
зависит от типа гидродвигателя. Самыми распространенными гидродвигателями являются гидромотор, в котором выходное звено совершает вращательное движение, и гидроцилиндр –гидродвигатель с возвратно-поступательным движением выходного звена.

Рисунок 2.10 – Гидромотор
Обозначение реверсивного гидромотора на схемах и параметры, характеризующие его работу, приведены на рисунке 2.10,
где 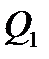 и
и 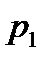 – параметры потока рабочей жидкости на входе в гидромотор;
– параметры потока рабочей жидкости на входе в гидромотор;
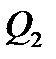 и
и 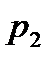 – параметры потока рабочей жидкости на выходе из гидромотора;
– параметры потока рабочей жидкости на выходе из гидромотора;
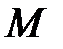 – момент сопротивления на валу гидромотора, как правило, направлен против вращения;
– момент сопротивления на валу гидромотора, как правило, направлен против вращения; 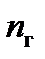 – частота вращения вала гидромотора.
– частота вращения вала гидромотора.
При расчете гидромотора можно использовать следующие формулы:
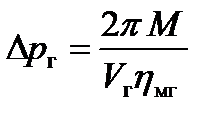 , (2.31)
, (2.31)
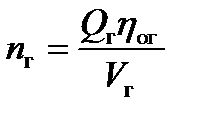 , (2.32)
, (2.32)
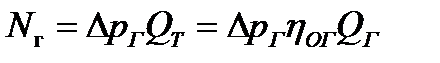 , (2.33)
, (2.33)
где 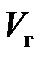 – рабочий объем гидромотора;
– рабочий объем гидромотора;
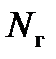 – мощность развиваемая гидромотором;
– мощность развиваемая гидромотором;
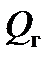 – расход рабочей жидкости через гидромотор;
– расход рабочей жидкости через гидромотор;
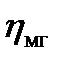 – механический к.п.д. гидромотора, значение которого в рабочем диапазоне скоростей и нагрузок может быть принято постоянным;
– механический к.п.д. гидромотора, значение которого в рабочем диапазоне скоростей и нагрузок может быть принято постоянным;
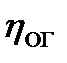 – объемныйк.п.д. гидромотора, который при известном перепаде давления
– объемныйк.п.д. гидромотора, который при известном перепаде давления 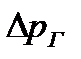 определяется по формуле
определяется по формуле
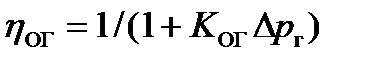 , (2.34)
, (2.34)
где 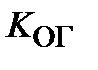 – коэффициент объемных потерь в гидромоторе.
– коэффициент объемных потерь в гидромоторе.
Для гидромоторов с достаточной степенью точности можно считать, что
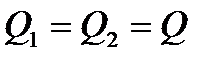 .
.
Дата добавления: 2017-11-21; просмотров: 1369;











