Расчёт основных параметров гидропривода
Пересечение полученной суммарной характеристики (2.41) сложного трубопровода с характеристикой насосной установки (2.22) определяет рабочую точку гидросистемы (точка 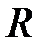 на рисунке 2.12).
на рисунке 2.12).
Координаты точки 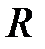 можно определить также путём решения системы равнений (2.22) и (2.41) для характеристик. Для её решения в системе Mathcad необходимо задать начальные значения искомых величин
можно определить также путём решения системы равнений (2.22) и (2.41) для характеристик. Для её решения в системе Mathcad необходимо задать начальные значения искомых величин
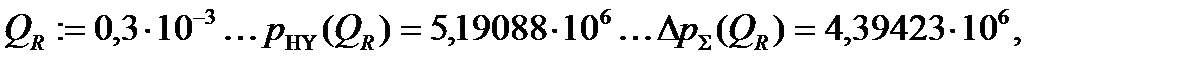
а затем записать само решение в виде Given-Find
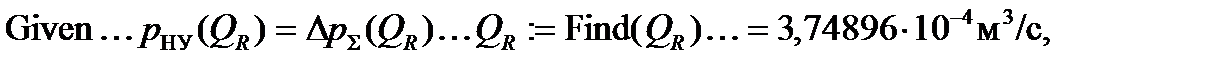
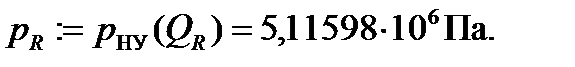
Итак, координаты рабочей точки гидросистемы:
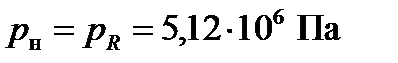 ,
, 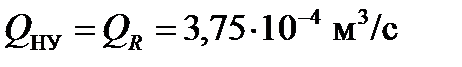 .
.
Поскольку рабочая точка 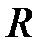 лежит на участке
лежит на участке 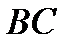 , то, согласно принципу работы регулируемого насоса с регулятором подачи, рабочая характеристика насоса изменяется и протекает по линии
, то, согласно принципу работы регулируемого насоса с регулятором подачи, рабочая характеристика насоса изменяется и протекает по линии 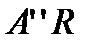 (см. рис. 2.12), параллельной линии
(см. рис. 2.12), параллельной линии 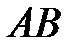 . С изменением рабочего объёма насоса соответственно изменяется и его теоретическая подача, которая будет равна
. С изменением рабочего объёма насоса соответственно изменяется и его теоретическая подача, которая будет равна 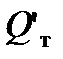 . Для определения
. Для определения 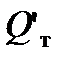 необходимо провести линию, параллельную линии
необходимо провести линию, параллельную линии 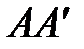 до пересечения с осью абсцисс.
до пересечения с осью абсцисс.
Это же можно сделать расчётным путём, если вычислить расход для точки 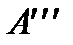 пересечения горизонтали, проходящей через точку
пересечения горизонтали, проходящей через точку 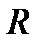 , с линией (1)
, с линией (1) 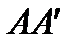 (в этом случае отрезки
(в этом случае отрезки 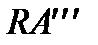 и
и 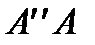 будут равны):
будут равны):
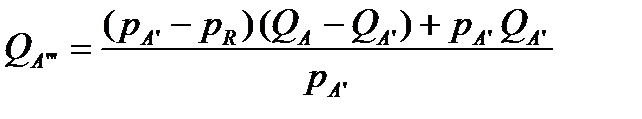 ,
, 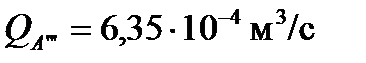 ,
,
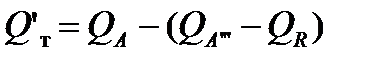 ,
, 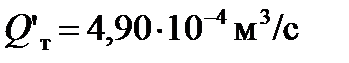 .
.
Потребляемую гидроприводом мощность определим по формуле для регулируемого насоса
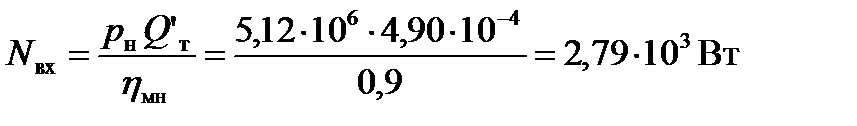 .
.
Для ответа на вопросы о скорости подъема грузов и коэффициенте полезного действия гидропривода, необходимо найти частоту вращения вала каждого гидромотора, т.е. найти значения расходов 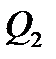 и
и  в простых трубопроводах 2 и 3.
в простых трубопроводах 2 и 3.
При этом исходят из того, что если графически построена зависимость 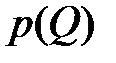 то по одной из известных координат легко находится другая.
то по одной из известных координат легко находится другая.
Опустив вертикаль из точки 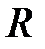 , соответствующую подаче насосной установки
, соответствующую подаче насосной установки 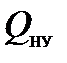 , находим точку
, находим точку 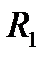 пересечения этой вертикали с кривой
пересечения этой вертикали с кривой 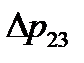 и, следовательно, потерю давления на параллельных участках
и, следовательно, потерю давления на параллельных участках 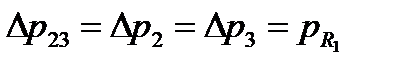 . Давление в точке
. Давление в точке 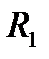 определяется уравнением характеристики
определяется уравнением характеристики 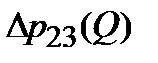 при расходе
при расходе 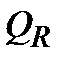 :
:
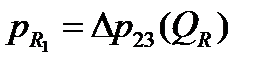 ,
,
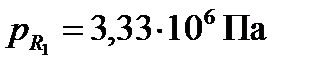 .
.
Проведя горизонталь через точку 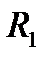 , соответствующую потерям давления
, соответствующую потерям давления 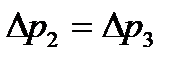 , находим точки пересечения этой прямой с зависимостями
, находим точки пересечения этой прямой с зависимостями 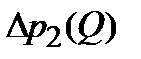 и
и 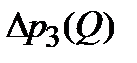 (соответственно точки
(соответственно точки 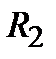 и
и 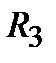 ).Опустив вертикали из точек
).Опустив вертикали из точек 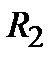 и
и 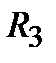 ,находим соответственно расходы.
,находим соответственно расходы.
Эти же расходы, но более точно можно найти, используя систему Mathcad, позволяющую отыскивать значения аргумента по заданному значению функции:
а) задаём начальные приближения 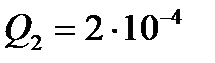 ,
, 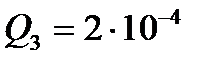 ;
;
б) решение 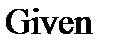
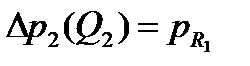 ,
,  ,
,
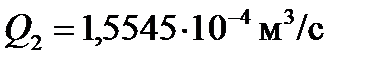 ;
;
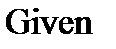
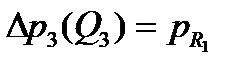 ,
, 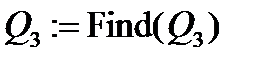 ,
, 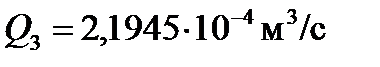 .
.
По известным расходам 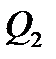 и
и  с учетом передаточного отношения механического редуктора и размеров шкива определяем скорости подъема левого
с учетом передаточного отношения механического редуктора и размеров шкива определяем скорости подъема левого 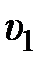 и правого
и правого 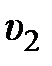 грузов. Из кинематики механизма подъема
грузов. Из кинематики механизма подъема
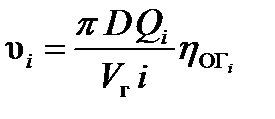 ,
,
где 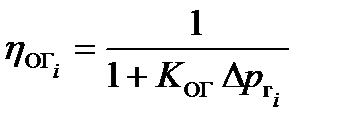 .
.
Тогда, подставив соответствующие значения, получим:
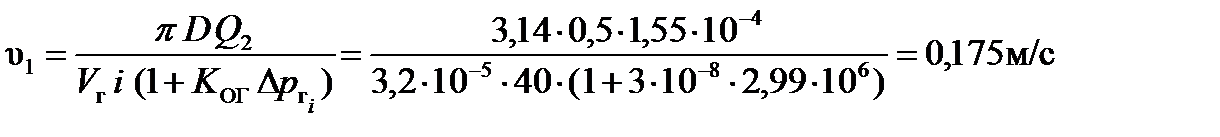 ;
;
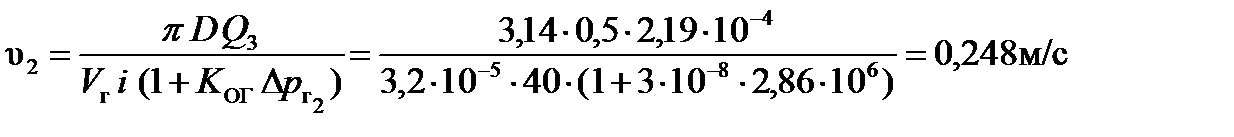 .
.
Полезная мощность, развиваемая гидроприводом, складывается из мощностей, затрачиваемых на подъем грузов,
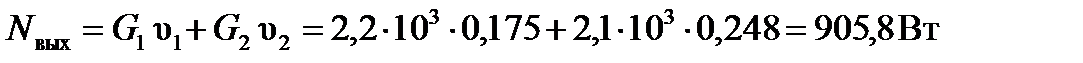 .
.
Коэффициент полезного действия гидропривода равен
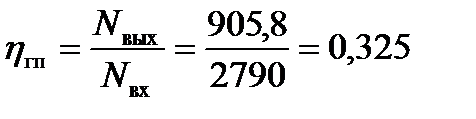 .
.
Дата добавления: 2017-11-21; просмотров: 1267;











