Электромагнитные волны, электромагнитное излучение — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля

электромагнитные волны подразделяются на:

· радиоволны (начиная со сверхдлинных),

· терагерцовое излучение,

· инфракрасное излучение,

· видимый свет,

· ультрафиолетовое излучение,

· рентгеновское излучение и жёсткое (гамма-излучение)

Электромагнитное излучение способно распространяться практически во всех средах. В вакууме (пространстве, свободном от вещества и тел, поглощающих или испускающих электромагнитные волны) электромагнитное излучение распространяется без затуханий на сколь угодно большие расстояния, но в ряде случаев достаточно хорошо распространяется и в пространстве, заполненном веществом (несколько изменяя при этом своё поведение).

Свойства электромагнитных волн.

Основными свойствами электромагнитных волн являются:

Поляризация для электромагнитных волн — явление направленного колебания векторов напряженности электрического поля e или напряженности магнитного поля h.

Рассеяние света — рассеяние электромагнитных волн видимого диапазона при их взаимодействии с веществом. При этом происходит изменение пространственного распределения, частоты, поляризации оптического излучения

Преломление — изменение направления распространения волн (лучей) электромагнитного излучения, возникающее на границе раздела двух прозрачных для этих волн сред или в толще среды с непрерывно изменяющимися свойствами.

Отражение — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл.

интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга

дифракция волн — явление, которое проявляет себя, как отклонение от законов геометрической оптики при распространении волн.

Поглощение электромагнитного излучения — процесс потери энергии потоком электромагнитного излучения вследствие взаимодействия с веществом, другими волнами или средой.

Энергия электромагнитных волн, поток энергии, плотность потока энергии. Вектор Пойнтинга. Полная энергия волны складывается из суммы электрической и магнитной энергий:

.

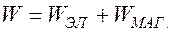Удобнее представлять энергию через объёмную плотность энергии волны:

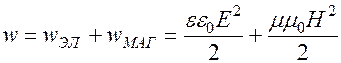
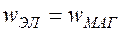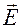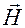Согласно закону сохранения энергии , т.к. Векторы и колеблются в одной фазе. Поэтому можно записать

.

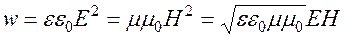Плотность потока энергии электромагнитной волны определяется как

.

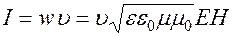Здесь 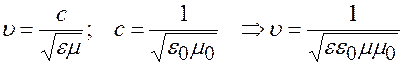; 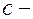скорость света в вакууме, поэтому

.

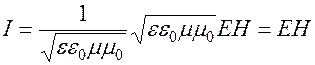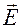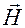Подставив значения векторов и , получим

,

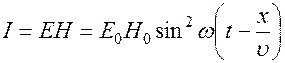А так выражается векторное произведение двух векторов, следовательно, 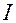является вектором:

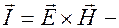вектор Умова-Пойнтинга, направлен в сторону распространения волны

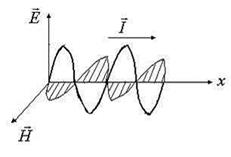
Шкала электромагнитных волн.

Длина электромагнитной волны связана с периодом (и частотой 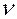) формулой

.

Световая волна. Интерференция световых волн. Когерентные волны. Условия максимума и минимума интерференции. Способы наблюдения интерференции света. Расчет интерференционной картины от двух линейных источников света.

Световая волна.

Световая волна - электромагнитная волна видимого диапазона длин волн. Частота световой волны (или набор частот) определяет ""цвет"". Энергия, переносимая световой волной, пропорциональна квадрату ее амплитуды.

Интерференция световых волн.

Опыт юнга является первым интерференционным опытом, получившим объяснение на основе волновой теории. В опыте юнга свет от источника проходит через две близко расположенные щели. Световые пучки, расширяясь из-за дифракции, падают на удаленный экран. В области перекрытия световых пучков возникают интерференционные полосы.

Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.

Когерентные волны.

Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Степень согласования может быть различной. Соответственно вводится понятие степени когерентности двух волн.

Пусть в данную точку пространства приходят две световые волны одинаковой частоты, которые возбуждают в этой точке колебания одинакового направления (обе волны поляризованы одинаковым образом):

Е = а₁соs(wt + a₁),

Е = a₂cos(wt + a₂), тогда амплитуда результирующего колебания

А² = а₁² +а₂² + 2а₁а₂соsj, (1)

Где j = a₁ - a₂ = const.

Если частоты колебаний в обеих волнах w одинаковы, а разность фаз j возбуждаемых колебаний остается постоянной во времени, то такие волны называются когерентными.

При наложении когерентных волн они дают устойчивое колебание с неизменной амплитудой а = соnst, определяемой выражением (1) и в зависимости от разности фаз колебаний лежащей в пределах |а₁ –а₂ê £ a £ а₁ +а_2.

Т.о., когерентные волны при интерференции друг с другом дают устойчивое колебание с амплитудой не больше суммы амплитуд интерферирующих волн.

Если j = p, тогда соsj = -1 и а₁ = а₂, a амплитуда суммарного колебания равна нулю, и интерферирующие волны полностью гасят друг друга.

В случае некогерентных волн j непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение <cоsj>_t = 0. Поэтому

А²> = <а₁²> + <а₂²>,

Откуда интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:

I = i₁ + i₂ .

В случае когерентных волн, соsj имеет постоянное во времени значение (но свое для каждой точки пространства), так что

I = i₁ + i₂ + 2ö i₁ × i₂ cosj (2)

Условия максимума и минимума интерференции.

Если разность хода равна целому числу длин волн в вакууме

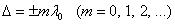(8.1.3)

То 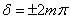, и колебания, возбуждаемые в точке р обеими волнами, будут происходить в одинаковой фазе. Следовательно, (8.1.3) является условием интерференционного максимума.

Если оптическая разность хода

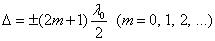(8.1.4)

То 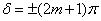, и колебания, возбуждаемые в точке р обеими волнами, будут происходить в противофазе. Следовательно, (8.1.4) является условием интерференционного минимума.

Способы наблюдения интерференции света.

Рассмотрим две конкретные интерференционные схемы, одна из которых использует для разделения световой волны на две части отражение, а другая – преломление света.

Зеркала Френеля. Два плоских соприкасающихся зеркала ом и on располагаются так, что их отражающие поверхности образуют угол, близкий кp (рис. 4.8), соответственно угол φ очень мал. Параллельно линии пересечения зеркал o на расстоянии r от нее помещается прямолинейный источник света s (например, узкая светящаяся щель). Зеркала отбрасывают на экран э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников s₁ и s₂. Непрозрачный экранэ₁преграждает свету пусть от источника s к экрану э.

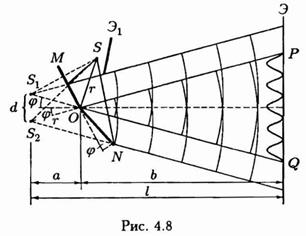
Луч oq представляет собой отражение луча so от зеркала ом, луч ор – отражение луча so от зеркала on. Легко сообразить, что угол между лучами ор и oq равен 2φ. Поскольку s и s₁ расположены относительно ом симметрично, длина отрезка os₁ равна os, т.е. r. Аналогичные рассуждения приводят к тому же результату для отрезкаos₂. Таким образом, расстояние между источникамиs₁иs₂равно

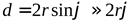
Из рис. 4.8 видно, что a=rcosφ»r. Следовательно,

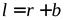
Где b– расстояние от линии пересечения зеркал o до экрана э.

Подставив найденные нами значения d и l в формулу (4.10), получим ширину интерференционной полосы:

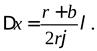(4.28)

Область перекрытия волн pq имеет протяженность 2b tgφ»2bφ. Разделив эту длину на ширину полосы δx, найдем максимальное число интерференционных полос, которое можно наблюдать с помощью зеркал френеля при данных параметрах схемы:

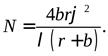(4.29)

Для того чтобы все эти полосы были действительно видны, необходимо, чтобы n/2 не превзошло m_пред, определяемого формулой (4.22).

Бипризма френеля.

Изготовленные из одного куска стекла две призмы с малым преломляющим углом Jимеют одну общую грань (рис. 4.9). Параллельно этой грани на расстоянии a от нее располагается прямолинейный источник света s.

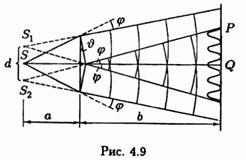
Можно показать, что в случае, когда преломляющий луч Jпризмы очень мал и углы падения лучей на грань призмы не очень велики, все лучи отклоняются призмой на практически одинаковой угол, равный

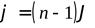
(n– показатель преломления призмы). Угол падения лучей на бипризму невелик. Поэтому все лучи отклоняются каждой из половин бипризмы на одинаковый угол. В результате образуются две когерентные цилиндрические волны, исходящие из мнимых источниковs₁иs₂, лежащих в одной плоскости сs. Расстояние между источниками равно

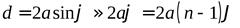
Расстояние от источников

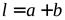
Ширину интерференционной полосы находим по формуле (4.10):

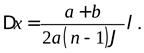(4.30)

Область перекрытия волн pq имеет протяженность

Максимальное число наблюдаемых полос составляет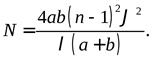

Расчет интерференционной картины от двух линейных источников света.

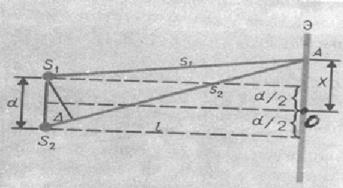
Расчет интерференционной картины для двух источников можно провести используя две узкие параллельные щели, расположенные достаточно близко друг к другу.

Щел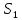и и 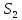находятся на расстоянии d друг от друга и являются когерентными источниками света. Интерференция наблюдается в произвольной точке а экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке о, симметричной относительно щелей. Интенсивность в любой точке а экрана, лежащей на расстоянии х от о, определяется оптической разностью хода 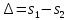(разностью оптических длин проходимых волнами путей). Из рисунка имеем: 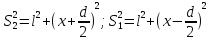откуда 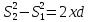или 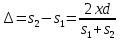. Из условия l>>d следует, что 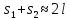поэтому 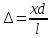. Подставив найденное значение δ в условия интерференционного максимума и минимума: 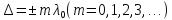и

, получим, что максимумы интенсивности будут наблюдаться при 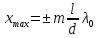, а минимумы – при 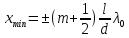. Расстояние между двумя соседними максимумами (или минимумами) называемое шириной интерференционной полосы равно: 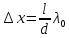. Δx не зависит от порядка интерференции (величины m) и является постоянной для 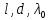. Δx обратно пропорционально d, след. При большом расстоянии между источниками, например, d ≈ l , отдельные полосы становятся неразличимыми. Из двух предпоследних формул следует так же, что интерференционная картина , создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m=0, проходит через точку о. Вверх и вниз от него, на равных расстояниях располагаются максимумы (минимумы) первого (m=1) и других порядков. Описанная картина справедлива только лишь при освещении монохроматическим светом. Если использовать белый свет, то интерференционные максимумы для каждой длины волны будут смещены друг относительно друга и иметь вид радужных полос. Только для m=0 максимумы всех длин волн совпадают, а в середине экрана будет наблюдаться белая полоса.