Явление отклонения световых волн от прямолинейного распространения при прохождении света мимо края препятствия получило название дифракции света.
Принцип гюйгенса – френеля.
Объяснить явление дифракции можно исходя из принципа гюйгенса-френеля. Этот принцип представляет собой правило, объясняющее, как, исходя из положения волнового фронта в данный момент, найти новое положение волнового фронта в последующий момент времени.
Гюйгенс предложил рассматривать каждую точку среды, которой достигла волна, как источник вторичных сферических волн, распространяющихся по всем направлениям со скоростью, присущей данной среде. Поверхность, огибающая вторичные волны, представляет собой фронт волны в данный момент времени.
Изложенное правило позволяет определить направление распространения волнового фронта, но не затрагивает вопроса о количественном распределении энергии дифрагировавшей волны. Этот недостаток был устранен френелем, который дополнил изложенный принцип следующим положением: вторичные сферические волны являются когерентными и колебания в любой точке пространства, которой вторичные волны достигнут в момент времени t , представляют собой результат интерференции этих вторичных волн. Т.о., правило распространения огибающей поверхности было заменено расчетом взаимной интерференции вторичных волн.
Зоны френеля.
Метод зон френеля. Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон френеля.
Пусть от источника света s распространяется монохроматическая сферическая волна, p - точка наблюдения. Через точку o проходит сферическая волновая поверхность. Она симметрична относительно прямой sp.
Разобьем эту поверхность на кольцевые зоны i, ii, iii и т.д. Так, чтобы расстояния от краев зоны до точки p отличались на l/2 - половину длины световой волны. Это разбиение было предложено o. Френелем и зоны называют зонами френеля.
Возьмем произвольную точку 1 в первой зоне френеля. В зоне ii найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку p от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке p.
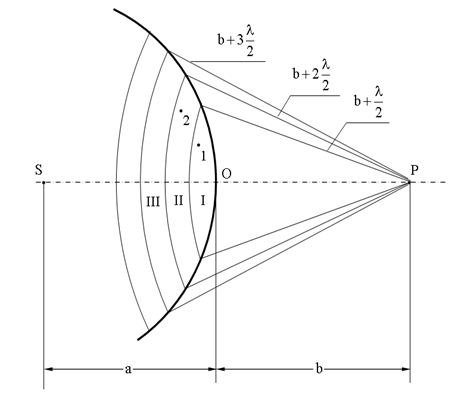
Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга.
Дифракция френеля на малом круглом отверстии.
Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса 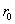 . Экран расположен так, что перпендикуляр, опущенный из s на непрозрачный экран, попадает точно в центр отверстия (рис. 9.3).
. Экран расположен так, что перпендикуляр, опущенный из s на непрозрачный экран, попадает точно в центр отверстия (рис. 9.3).
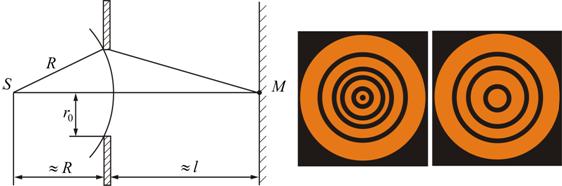
Рис. 9.3
На продолжении этого перпендикуляра возьмем точку m и рассмотрим, что мы будем наблюдать на экране.
Разобьем открытую часть волновой поверхности на зоны френеля. Вид дифракционной картины зависит от числа зон френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке м всеми зонами (9.2.1) и (9.2.2),
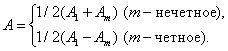
| (9.3.1) |
Таким образом, когда отверстие открывает нечетное число зон френеля, то амплитуда (интенсивность) в точке м будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю, как показано на рис. 9.3.
Естественно, что если 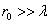 , то никакой дифракционной картины не будет.
, то никакой дифракционной картины не будет.
Дифракция Фраунгофера на одной щели.
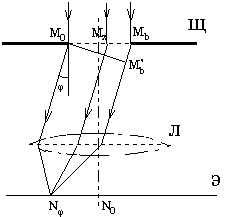
Рассмотрим схему наблюдения дифракции Фраунгофера, представленную на рис.3. Плоская монохроматическая волна падает нормально на плоскость щ, где расположена бесконечно длинная щель шириной b (щель можно считать бесконечно длинной, если ее длина намного больше ее ширины. Так при ширине в 0,01 - 0,05 мм длина в несколько миллиметров может считаться бесконечной).
За щелью расположена линза л, в фокальной плоскости которой находится экран э. Наличие линзы равносильно тому, что экран расположен как бы на "бесконечном" расстоянии от объекта. Если бы свет распространялся прямолинейно в соответствии с законами геометрической оптики, то в фокальной плоскости линзы получилась бы бесконечно узкая светлая полоса, проходящая через точку n0 на экране э. Но в соответствии с принципом гюйгенса-френеля каждая точка волнового фронта, достигающего плоскости, где расположена щель, является источником вторичных волн. Тогда лучи, идущие от всех этих вторичных источников под некоторым углом к первоначальному направлению, образуют плоский волновой фронт и соберутся в фокальной плоскости линзы в т.n (рис.3).
|
| Рис.3. Дифракция Фраунгофера на одной щели. |
Расчет поля в плоскости экрана проведём непосредственно на основе принципа гюйгенса-френеля, не используя формулу (1). Для этого разобьем открытую часть поверхности щели на зоны в виде узких полосок одинаковой ширины dх, параллельных краям щели. Эти элементарные участки становятся источниками вторичных волн. Амплитуды da0 этих волн, приходящих в т. N на экране от разных полосок, одинаковы, так как все зоны имеют одинаковую площадь и одинаковый к направлению вторичных волн угол . Эти амплитуды будут пропорциональны произведению амплитуды падающей волны е0 на размер полоски dx, т.е.
Da0 = ce0 dx (2)
Где с - коэффициент пропорциональности.
Однако фазы колебаний, приходящих от различных участков щели, будут различаться. Для определения разности фаз проведем прямую м0мb', перпендикулярную к направлению дифрагированных лучей, и найдем разность хода, возникающую на пути от прямой м0мb до прямой м0мb'. Из рис.3 видно, что разность хода между волнами, идущими от точки м0 и от точки мх, расположенной на расстоянии х от т.м0, равна хsin.
Следовательно, если считать, что фаза волны, приходящей в т. N из т.м0, равна нулю, то колебание du, приходящее от элемента dх из окрестности точки мхв т. N, может быть записано в виде:
Du = dа0 cos(t-kxsin)
Где k=2/ - волновое число, - частота колебания.
Для вычисления величины u в т. N необходимо просуммировать вклады от различных участков щели, т.е. Проинтегрировать du в пределах от х = 0 до х = b:
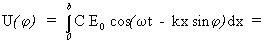
|
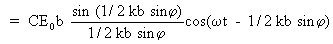 (3) (3)
|
Сомножитель cos(t-1/2kbsin) в формуле (3) описывает временное изменение поля в точке наблюдения с частотой , а модуль выражения, стоящего перед косинусом, есть амплитуда a результирующей волны в точке n :
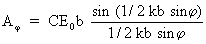 (4) (4)
|
Отметим, что амплитуда волны, распространяющейся в направлении =0, пропорциональна ширине щели b и равна
A0=ce0b (5)
И выражение (4) можно переписать в виде
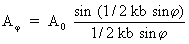 (4') (4')
|
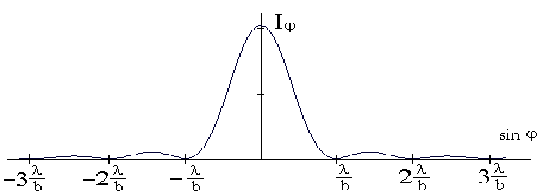
Интенсивность света определяется квадратом амплитуды, т.е.
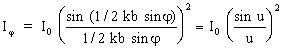 (6) (6)
|
Где i0 - интенсивность в центре дифракционной картины, u =1/2 kbsin.
|
Дифракция Фраунгофера на дифракционной решетке.
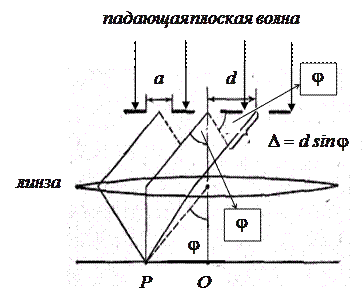
Рисунок 6.4.2. – схема установки для дифракции Фраунгофера
на дифракционной решетке.
Дифракционной решеткой называется совокупность большого числа узких одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей (рисунок 6.4.2). Расстояние d между серединами соседних щелей называется периодом решетки. Период решетки равен сумме ширины щели а и расстояния между щелями b, т.е. 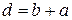 . Решетка также характеризуется числом штрихов на единицу длины
. Решетка также характеризуется числом штрихов на единицу длины 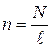 , где n – полное число штрихов в решетке,
, где n – полное число штрихов в решетке, 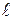 – длина решетки.
– длина решетки.
· Условие для главных максимумов дифракционной картины от дифракционной решетки 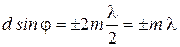 , где
, где 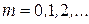 между соседними главными максимумами лежат прежний минимум и
между соседними главными максимумами лежат прежний минимум и 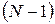 добавочный минимум, где n– число щелей в решетке. Эти минимумы возникают в тех направлениях, для которых колебания от всех щелей взаимно гасят друг друга, т.к. Сложение амплитуд колебаний от отдельных щелей векторное. Условия прежнего минимума
добавочный минимум, где n– число щелей в решетке. Эти минимумы возникают в тех направлениях, для которых колебания от всех щелей взаимно гасят друг друга, т.к. Сложение амплитуд колебаний от отдельных щелей векторное. Условия прежнего минимума 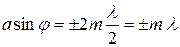 . Условия для добавочных минимумов имеет вид:
. Условия для добавочных минимумов имеет вид: 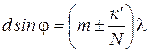 , где
, где 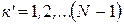 . Положение главных максимумов зависит от длины волны
. Положение главных максимумов зависит от длины волны 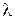 . Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный расположен дальше от центра, чем фиолетовый. Центральный максимум будет белого цвета.
. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный расположен дальше от центра, чем фиолетовый. Центральный максимум будет белого цвета.
Дата добавления: 2017-11-21; просмотров: 2368;











