Интерференция света в тонких плёнках. Полосы равного наклона и равной толщины. Кольца ньютона. Практическое применение интерференции.

Интерференция света в тонких плёнках.

Интерференцию света можно наблюдать не только в лабораторных условиях с помощью специальных установок и приборов, но и в ес­тественных условиях. Так, легко наблюдать радужную окраску мыльных пленок, тонких пленок нефти и минерального масла на поверхности воды, оксидных пленок на поверхности закаленных стальных деталей (цвета побежалости). Все эти явления обусловле­ны интерференцией света в тонких прозрачных пленках, возникающей в результате наложения когерентных волн, возникающих при отражении от верхней и нижней по­верхностей пленки.

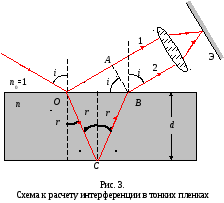
Оптическая разность хода лучей 1 и 2

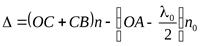(6)

Где п – показатель преломления пленки; n₀ – показатель прелом­ления воздуха, n₀ = 1; λ₀/2 – длина полуволны, потерянной при от­ражении луча 1 в точке о от границы раздела с оптически более плотной средой (n >n₀,).

;

;

;

.

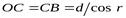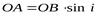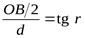
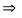
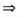
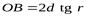
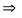
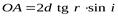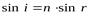
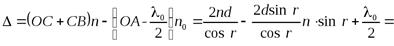
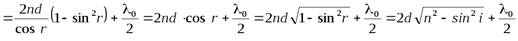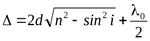. (7)

Полосы равного наклона и равной толщины.

Полосы равной толщины и равного наклона наблюдаются при интерференции волн, отраженных от двух границ прозрачной пленки или плоскопараллельной пластинки.

Полосы равного наклона локализованы на бесконечности.

Полосы равной толщины локализованы в плоскости, отражающей пленки. В пределах ширины пленки можно считать, что интерференционная картина локализована там, где вам удобнее.

Для наблюдения полос равной толщины отражающие поверхности не обязательно должны быть идеально плоскопараллельны. Пара отражающих плоскостей может образовывать тонкий клин. Могут быть соприкасающиеся поверхности, одна или обе из которых сферические (кольца ньютона).

Более того, две отражающих поверхности могут быть расположены в разных местах, как в интерферометре майкельсона (рис.28). Здесь s — источник света, p — экран для наблюдения интерференции отраженных волн от зеркал 1 и 2, 3 — полупрозрачная пластинка. Если зеркало 2 мысленно отразить в полупрозрачной пластинке 3, то его изображение примет положение 2'. Вместе с зеркалом 2 мысленно отобразим в полупрозрачной пластинке и все лучи, идущие справа от нее к зеркалу 2 и от него обратно к полупрозрачной пластинке. Тогда на экран p свет будет приходить, как бы отражаясь от двух плоскостей 1 и 2'. Если дополнить интерферометр двумя линзами, как это обычно делается (рис. 29), то, в зависимости от расстояния между линзой l₂и экраном p, можно наблюдать полосы равной толщины (1/a₁+ 1/a₂= 1/f₂) или полосы равного наклона (a₂= f₂).

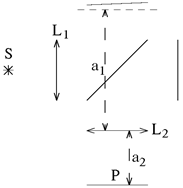
Рис. 29

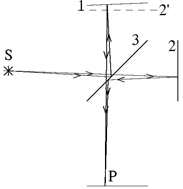
Рис. 28

Кольца ньютона.

К 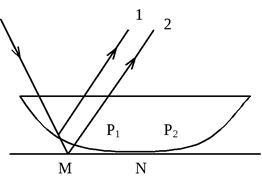ольца ньютона представляют собой интерференционные полосы, возникающие при наложении волн, отраженных от верхней и нижней поверхностей тонкой воздушной прослойки, заключенной между стеклянной пластинкой и наложенной на нее линзой большого радиуса кривизны (рис.2).

Ширина воздушного слоя увеличивается от точки соприкосновения n к краям линзы. В точках p₁ и p₂, равноотстоящих от точки n, толщина слоя одинакова. На всей поверхности пластины равные толщины слоя располагаются по концентрическим окружностям с центром в точке n. Если осветить систему пластинка - линза почти параллельным пучком монохроматческого света., то в отраженном свете наблюдается большое число чередующихся светлых и темных концентрических колец с темным пятном в области точки n. Эти полосы равной толщины называются кольцами ньютона. Темное пятно в центре колец (при наблюдении в отраженном свете) объясняется тем, что геометрическая разность хода между интерферирующими волнами в области точки n практически равна нулю и лишь теряется полуволна 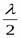при отражении от поверхности линзы.

Разность хода интерферирующих волн 1 и 2 D = 2d×n. Для воздушного слоя n = 1. Кроме указанной разности хода появляется дополнительная разность хода в полволны 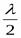вследствие отражения луча в точке м от оптически более плотной среды:

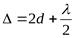(8)

Таким образом, полная разность хода между волнами 1 и 2 будет:

1). Для темных колец 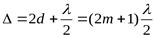(9)

2). Для светлых колец 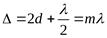(10)

Где m = 1,2,3…

Рассчитаем радиусы колец ньютона r_m, наблюдаемых в отраженном свете.

Рис.3

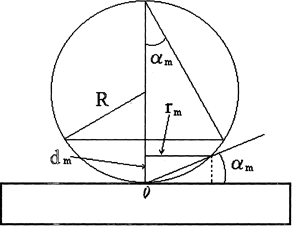
из рис.3 следует, что для кольца порядка m:

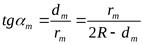
Так как d_m<<2r, то 2r-d_m 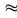2r следовательно:

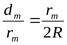
Откуда

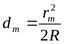(11)

Подставляя в формулы (9) и (10) выражение для d_m получим:

1). Для темных колец 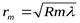(12)

2). Для светлых колец 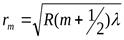(13)

Из этих формул можно было бы определить l, зная радиус кольца, радиус кривизны линзы и порядок минимума (или максимума). Однако вследствие упругой деформации стекла невозможно добиться идеального соприкосновения линзы и пластинки в точке о. Поэтому более точно результат получится, если вычислять l по разности диаметров двух колец порядка d_k и d_m. Для темных колец имеем:

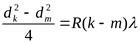
Откуда

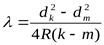(14)

Таким образом, зная радиус кривизны линзы и диаметры темных интерференционных колец:, можно по формуле (14) вычислить длину световой волны l.

Практическое применение интерференции.

Использование интерференции в технике. Явление интерференции света находит широкое применение в современной технике. Одним из таких применений является создание "просветленной" оптики. Отполированная поверхность стекла отражает примерно 4% падающего на нее света. Современные оптические приборы состоят из большого числа деталей, изготовленных из стекла. Проходя через каждую из этих деталей, свет ослабляется на 4%. Общие потери света в объективе фотоаппарата составляют примерно 25%, в призменном бинокле и микроскопе - 50% и т. Д.

Для уменьшения световых потерь в оптических приборах все стеклянные детали , через которые проходит свет, покрывают пленкой, показатель преломления которой меньше показателя преломления стекла. Толщина пленки равна четверти длины волны.

Другим применением явления интерференции является получение хорошо отражающих покрытий, необходимых во многих отраслях оптики. В этом случае используют тонкую пленку толщиной l/4 из материала, коэффициент преломления которого n ₂ больше коэффициента преломления n ₃ . В этом случае отражение от передней границы происходит с потерей полволны, так как n ₁ < n ₂ , а отражение от задней границы происходит без потери полволны (n ₂ > n ₃ ). В результате разность хода d = l/4+l/4+l/2=l и отраженные волны усиливают друг друга.

И. С. Широко используется при спектральном анализе для точного измерения расстояний и углов, в рефрактометрии, в задачах контроля кач-ва поверхностей, для создания светофильтров, зеркал, просветляющих покрытий и др.; на явлениях и. С. Основана голография. Важный случай и. С. - интерференция поляризованных лучей.

Дифракция света. Принцип Гюйгенса – Френеля. Зоны Френеля. Дифракция Френеля на малом круглом отверстии. Дифракция Фраунгофера на одной щели. Дифракция Фраунгофера на дифракционной решетке. Дисперсия и разрешающая способность дифракционной решетки.

Дифракция света.